
【题目】如图,在△ABC中,AC=BC,∠ACB=![]() ,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
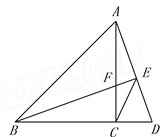
(1)求证: CF=CD;
(2)求证: ![]() ;
;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
【答案】(1)证明见解析(2)证明见解析(3)AE,BE,CE之间满足的等量关系![]()
【解析】试题分析:(1)由垂直的定义得到∠ACB=90°,根据全等三角形的判定定理ASA可证明△BCF≌△ACD,然后根据全等三角形的性质可证明;
(2)根据相似三角形的判定证得△BED∽△ACD,然后根据相似三角形的性质可证明;
(3)在BE上截取BG=AE,连接CG,然后根据三角形全等的判定可证明△GCE是等腰直角三角形,由此可得到结果.
试题解析:(1)证明:∵∠BCA=∠ACD = 90°
∴∠FBC+∠D=∠CAD +∠D = 90°
∴∠FBC =∠CAD
∵AC=BC
∴△BCF≌△ACD(ASA)
∴CF=CD
(2)证明:∵∠FBC =∠CAD ∠D=∠D
∴△BED∽△ACD
∴BD:AD=ED:CD
∴![]()
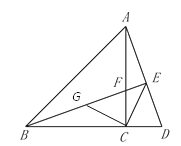
(3)AE,BE,CE之间满足的等量关系![]()
理由:在BE上截取BG=AE,连接CG,
∵∠FBC =∠CAD BC=AC
∴△BCG≌△ACE
∴GC=EC 且∠BCG=∠ACE
∴∠GCE=∠ACD= 90°
∴△GCE为等腰直角三角形
∴GC=![]() CE
CE
∴![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】港珠澳大桥全长约为55000米,将数据55000科学记数法表示为( )
A. 0.55×105B. 5.5×104C. 55×103D. 550×102
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的对角线相交于点O,AC=![]() ,CD=1,
,CD=1,
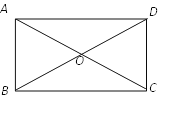
(1)尺规作图:作∠ABC的平分线交AD于点E,连结CE;
(2)判断线段BE与CE的关系,并证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解初三女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
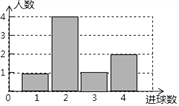
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有初三女生400人,从中任选一位女生,求选到的女生投篮成绩为“优秀”等级的的概率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
①S△ADB=S△ADC;
②当0<x<3时,y1<y2;
③如图,当x=3时,EF=![]() ;
;
④当x>0时,y1随x的增大而增大,y2随x的增大而减小.
其中正确结论的个数是( )
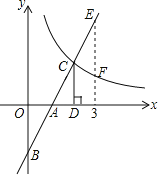
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若把代数式x2-2x+3化为(x-m)2+k的形式,其中m,k为常数,结果正确的是( )
A. (x+1)2+4 B. (x-1)2+2 C. (x-1)2+4 D. (x+1)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com