
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
①S△ADB=S△ADC;
②当0<x<3时,y1<y2;
③如图,当x=3时,EF=![]() ;
;
④当x>0时,y1随x的增大而增大,y2随x的增大而减小.
其中正确结论的个数是( )
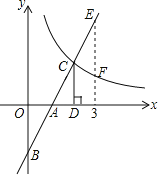
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】试题分析:对于直线解析式,分别令x与y为0求出y与x的值,确定出A与B坐标,利用AAS得到三角形OBA与三角形CDA全等,利用全等三角形对应边相等得到CD=OB,确定出C坐标,代入反比例解析式求出k的值,确定出反比例解析式,由图象判断y1<y2时x的范围,以及y1与y2的增减性,把x=3分别代入直线与反比例解析式,相减求出EF的长,即可做出判断.
解:对于直线y1=2x﹣2,
令x=0,得到y=﹣2;令y=0,得到x=1,
∴A(1,0),B(0,﹣2),即OA=1,OB=2,
在△OBA和△CDA中,
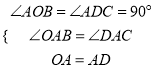 ,
,
∴△OBA≌△CDA(AAS),
∴CD=OB=2,OA=AD=1,
∴S△ADB=S△ADC(同底等高三角形面积相等),选项①正确;
∴C(2,2),
把C坐标代入反比例解析式得:k=4,即y2=![]() ,
,
由函数图象得:当0<x<2时,y1<y2,选项②错误;
当x=3时,y1=4,y2=![]() ,即EF=4﹣
,即EF=4﹣![]() =
=![]() ,选项③正确;
,选项③正确;
当x>0时,y1随x的增大而增大,y2随x的增大而减小,选项④正确,
故选C


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=![]() ,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
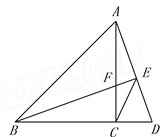
(1)求证: CF=CD;
(2)求证: ![]() ;
;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解七年级同学对三种元旦活动方案的意见,校学生会对七年级全体同学进行了一次调查(每人至多赞成一种方案).结果有115人赞成方案1,62人赞成方案2,40人赞成方案3,8人弃权,请用扇形图描述这些数据,并对校学生会采用的哪种方案组织元旦活动提出建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )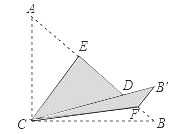
A.![]()
B.6
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+![]() x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+![]() x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;
(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com