
【题目】为了解七年级同学对三种元旦活动方案的意见,校学生会对七年级全体同学进行了一次调查(每人至多赞成一种方案).结果有115人赞成方案1,62人赞成方案2,40人赞成方案3,8人弃权,请用扇形图描述这些数据,并对校学生会采用的哪种方案组织元旦活动提出建议.
 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的直径为5,sinA=![]() ,求BH的长.
,求BH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的对角线相交于点O,AC=![]() ,CD=1,
,CD=1,
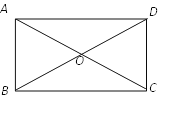
(1)尺规作图:作∠ABC的平分线交AD于点E,连结CE;
(2)判断线段BE与CE的关系,并证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
①S△ADB=S△ADC;
②当0<x<3时,y1<y2;
③如图,当x=3时,EF=![]() ;
;
④当x>0时,y1随x的增大而增大,y2随x的增大而减小.
其中正确结论的个数是( )
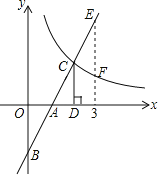
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,A,B两点的坐标分别为A(x1,y1),B(x2,y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A,B两点间的距离为:AB=![]() 我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xoy中,A(x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.
我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xoy中,A(x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.
问题拓展:如果圆心坐标为P(a,b),半径为r,那么⊙P的方程可以写为 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使∠POA=30°,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明:AB是⊙P的切线;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以Q为圆心,以OQ为半径的⊙Q的方程;若不存在,说明理由.
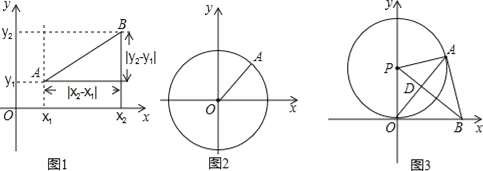
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各项是真命题的是( )
A. 从直线外一点到已知直线的垂线段叫做这点到直线的距离
B. 过一点有且只有一条直线与已知直线平行
C. 有公共顶点且相等的两个角是对顶角
D. 同一平面内,不重合的两条直线的位置关系只有相交和平行两种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com