
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )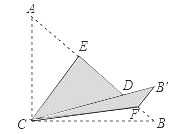
A.![]()
B.6
C.![]()
D.![]()
【答案】C
【解析】根据折叠的性质可知:DE=AE,∠ACE=∠DCE,∠BCF=∠B′CF,CE⊥AB,B′F=BF,
∴B′D=4-3=1,∠DCE+∠B′CF=∠ACE+∠BCF,
∵∠ACB=90°,
∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B′FC=135°,
∴∠B′FE=90°,
∵S△ABC= ![]() ACBC=
ACBC= ![]() ABCE,
ABCE,
∴ACBC=ABCE,
∵根据勾股定理得:AB= ![]() =10,
=10,
∴CE= ![]() =4.8,
=4.8,
∴EF=4.8,AE= ![]() =3.6,
=3.6,
∴B′F=BF=AB-AE-EF=10-3.6-4.8=1.6,
∴B′E= ![]() .
.
所以答案是:C.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】某校随机抽取了八年级50名男生立定跳远的测试成绩,根据如下统计表,可求得( )
等级 | 成绩(分) | 频数(人数) | 频率 |
A | 90~100 | 19 | 0.38 |
B | 75~89 | 20 | x |
C | 60~74 | n | y |
D | 60以下 | 3 | 0.06 |
合计 | 50 | 1.00 |
A.n=8,x=0.4
B.n=8,x=0.16
C.n=8,x=0.5
D.n=8,x=0.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的对角线相交于点O,AC=![]() ,CD=1,
,CD=1,
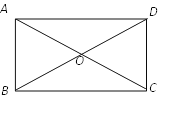
(1)尺规作图:作∠ABC的平分线交AD于点E,连结CE;
(2)判断线段BE与CE的关系,并证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
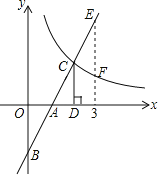
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
①S△ADB=S△ADC;
②当0<x<3时,y1<y2;
③如图,当x=3时,EF=![]() ;
;
④当x>0时,y1随x的增大而增大,y2随x的增大而减小.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
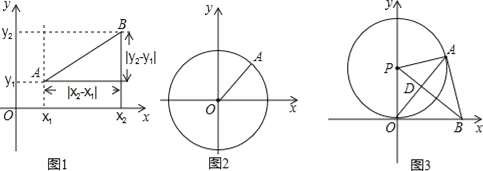
【题目】如图1,在平面直角坐标系xOy中,A,B两点的坐标分别为A(x1,y1),B(x2,y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A,B两点间的距离为:AB=![]() 我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xoy中,A(x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.
我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xoy中,A(x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.
问题拓展:如果圆心坐标为P(a,b),半径为r,那么⊙P的方程可以写为 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使∠POA=30°,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明:AB是⊙P的切线;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以Q为圆心,以OQ为半径的⊙Q的方程;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若把代数式x2-2x+3化为(x-m)2+k的形式,其中m,k为常数,结果正确的是( )
A. (x+1)2+4 B. (x-1)2+2 C. (x-1)2+4 D. (x+1)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各项是真命题的是( )
A. 从直线外一点到已知直线的垂线段叫做这点到直线的距离
B. 过一点有且只有一条直线与已知直线平行
C. 有公共顶点且相等的两个角是对顶角
D. 同一平面内,不重合的两条直线的位置关系只有相交和平行两种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com