
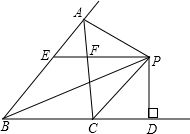
 ��ͼ����ABC�У���ABC��ƽ�������ACB����ǵ�ƽ�����ཻ�ڵ�P������P��BC��ƽ���߽�AB��AC�ֱ��ڵ�E��F����PD��BC�ڵ�D�����������������ۣ�
��ͼ����ABC�У���ABC��ƽ�������ACB����ǵ�ƽ�����ཻ�ڵ�P������P��BC��ƽ���߽�AB��AC�ֱ��ڵ�E��F����PD��BC�ڵ�D�����������������ۣ�| A�� | 3 | B�� | 2 | C�� | 1 | D�� | 0 |
���� �ɽ�ƽ���ߺ������ε�������ʵó�����ȷ��
��FC��FP�ó��Ե�EΪԲ�ģ�EBΪ�뾶��Բ���Ե�FΪԲ�ġ�FCΪ�뾶��Բ�����У��ó��ڲ���ȷ��
ͨ�������AEF������ó��۲���ȷ��
��� �⣺����ȷ��
�ߡ�ABC��ƽ�������ACB����ǵ�ƽ�����ཻ�ڵ�P��
���ABP=��CBP=$\frac{1}{2}$��ABC����PCD=$\frac{1}{2}$��ACD��
�ߡ�ACD=��ABC+��BAC����PCD=��CBP+��BPC��
��2����CBP+��BPC��=��ABC+��BAC��
���BPC=$\frac{1}{2}$��BAC��
�����ȷ��
�ڲ���ȷ��
��FC��FP��
���Ե�EΪԲ�ģ�EBΪ�뾶��Բ���Ե�FΪԲ�ġ�FCΪ�뾶��Բ�����У�
��ڲ���ȷ��
�۲���ȷ��
�ߡ�AEF�����=$\frac{1}{2}$AE•PD-$\frac{1}{2}$AF•PD=$\frac{1}{2}$mn��
��۲���ȷ��
��ȷ�ĸ�����1����
��ѡ��C��
���� ���⿼�������ߵ��ж�����ƽ���ߡ������ε�������ʡ�����������ļ��㣻�������ս�ƽ���ߵ����ʺ������ε�������ʣ����ܽ������������ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | ͬ�ȴ�С | C�� | 2�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | -1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
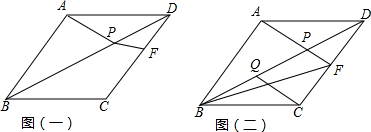
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
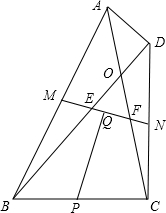 ��ͼ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AC=BD��M��P��N�ֱ��DZ�AB��BC��CD���е㣬Q��MN���е㣮
��ͼ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AC=BD��M��P��N�ֱ��DZ�AB��BC��CD���е㣬Q��MN���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com