
【题目】如图,正方形 ABCD 中,AB=3cm,以 B 为圆心,1cm 长为半径画☉B,点 P 在☉B 上移动,连接 AP,并将 AP 绕点 A 逆时针旋转 90°至 AP',连接 BP',在点 P 移动过程中,BP' 长度的最小值为________cm。

【答案】3![]() -1
-1
【解析】
通过画图发现,点P′的运动路线为以D为圆心,以1为半径的圆,可知:当P′在对角线BD上时,BP′最小,先证明△PAB≌△P′AD,则P′D=PB=1,再利用勾股定理求对角线BD的长,则得出BP′的长.

如图,当P′在对角线BD上时,BP′最小,
连接BP,
由旋转得:AP=AP′,∠PAP′=90°,
∴∠PAB+∠BAP′=90°,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BAP′+∠DAP′=90°,
∴∠PAB=∠DAP′,
∴△PAB≌△P′AD,
∴P′D=PB=1,
在Rt△ABD中,∵AB=AD=3,
由勾股定理得:BD=![]() =
=![]() ,
,
∴BP′=BDP′D=![]() 1,
1,
即BP′长度的最小值为![]() 1cm.
1cm.
故答案为:![]() 1.
1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角尺按如图①方式拼接:含30°角的三角尺的长直角边与含45°角的三角尺的斜边恰好重合(在Rt△ABC中,∠ACB=90°,∠BAC=30°;在Rt△ACD中,∠ADC=90°∠DAC=45°)已知AB=2![]() ,P是AC上的一个动点.
,P是AC上的一个动点.

(1)当PD=BC时,求∠PDA的度数;
(2)如图②,若E是CD的中点,求△DEP周长的最小值;
(3)如图③,当DP平分∠ADC时,在△ABC内存在一点Q,使得∠DQC=∠DPC,且CQ=![]() ,求PQ的长.
,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:射线![]() 交
交![]() 于点
于点![]() ,半径
,半径![]() ,
,![]() 是射线
是射线![]() 上的一个动点(不与
上的一个动点(不与![]() 、
、![]() 重合),直线
重合),直线![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 的切线交射线
的切线交射线![]() 于
于![]() .
.
![]() 图
图![]() 是点
是点![]() 在圆内移动时符合已知条件的图形,在点
在圆内移动时符合已知条件的图形,在点![]() 移动的过程中,请你通过观察、测量、比较,写出一条与
移动的过程中,请你通过观察、测量、比较,写出一条与![]() 的边、角或形状有关的规律,并说明理由;
的边、角或形状有关的规律,并说明理由;
![]() 请你在图
请你在图![]() 中画出点
中画出点![]() 在圆外移动时符合已知条件的图形,第
在圆外移动时符合已知条件的图形,第![]() 题中发现的规律是否仍然存在?说明理由.
题中发现的规律是否仍然存在?说明理由.
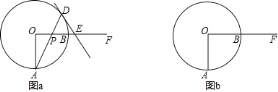
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A点的坐标为(﹣1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐 标为(3,﹣1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B分别在x轴负半轴和y轴正半轴上,点C(2,-2),CA、CB分别交坐标轴于D、E,CA⊥AB,且CA=AB.
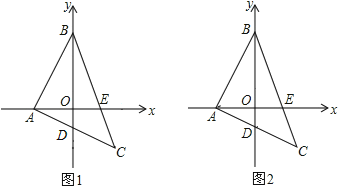
(1)求点B的坐标;
(2)如图2,连接DE,求证:BD-AE=DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有【 】个.

A.2 B.3 C.4 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com