Question

【题目】点A、B分别在x轴负半轴和y轴正半轴上，点C（2，－2），CA、CB分别交坐标轴于D、E，CA⊥AB，且CA=AB.

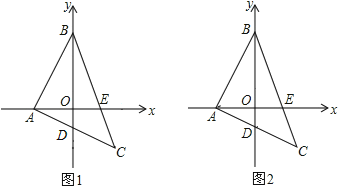
（1）求点B的坐标；

（2）如图2，连接DE，求证：BD－AE=DE.

Answer 1

【答案】（1）B（0，4）；（2）见解析

【解析】

（1）作CM⊥x轴于M，求出CM=OM=2，利用AAS证出△BAO≌△ACM，得出AO=CM=2，OB=AM=4，即可得出答案；
（2）在BD上截取BF=AE，连AF，证△BAF≌△CAE，证△AFD≌△CED，即可得出答案．

解：（1）如图1，作CM⊥x轴于M，

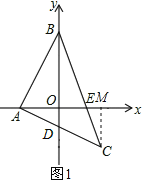
∵C（2，-2），
∴CM=2，OM=2，
∵AB⊥AC，
∴∠BAC=∠AOB=∠CMA=90°，
∴∠BAO+∠CAM=90°，∠CAM+∠ACM=90°，
∴∠BAO=∠ACM，
在△BAO和△ACM中

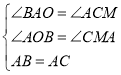
∴△BAO≌△ACM，
∴AO=CM=2，OB=AM=AO+OM=2+2=4，
∴B（0，4）．
（2）证明：如图2，在BD上截取BF=AE，连AF，

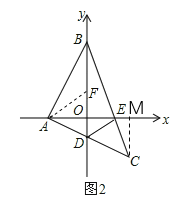
∵△BAO≌△CAM，
∴∠ABF=∠CAE，
在△ABF和△ACE中，

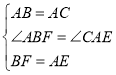
∴△ABF≌△CAE（SAS），
∴AF=CE，∠ACE=∠BAF=45°，
∵∠BAC=90°，
∴∠FAD=45°=∠ECD，
由（1）可知OA=OM，OD∥CM，
∴AD=DC，（图1中），
在△AFD和△CED中，

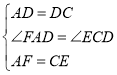
∴△AFD≌△CED（SAS），
∴DE=DF，
∴BD-AE=DE；