
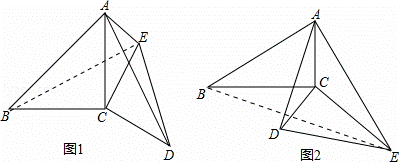
(1)如图1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
(2)如图2,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长.
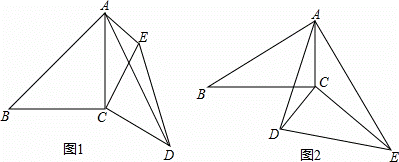
解:(1)如图1,连接BE,
∵∠ACB=∠DCE=90°,
∴∠ACB+∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,
又∵AC=BC,DC=EC,
在△ACD和△BCE中,
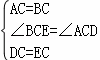 ,
,
∴△ACD≌△BCE,
∴AD=BE,
∵AC﹣BC=6,
∴AB=6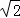 ,
,
∵∠BAC=∠CAE=45°
∴∠BAE=90°,
在Rt△BAE中,AB=6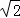 ,AE=3,
,AE=3,
∴BE=9,
∴AD=9;
(2)如图2,连接BE,
在Rt△ACB中,∠ABC=∠CED=30°,
tan30°=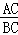 =
=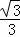 ,
,
∵∠ACB=∠DCE=90°,
∴∠BCE=∠ACD,
∴△ACD∽△BCE,
∴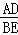 =
=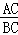 =
=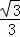 ,
,
∵∠BAC=60°,∠CAE=30°,
∴∠BAE=90°,又AB=6,AE=8,
∴BE=10,
∴AD=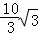 .
.


科目:初中数学 来源: 题型:
直线a、b、c、d的位置如图所示,如果∠1=58°,∠2=58°,∠3=70°,那么∠4等于( )

|
| A. | 58° | B. | 70° | C. | 110° | D. | 116° |
查看答案和解析>>
科目:初中数学 来源: 题型:
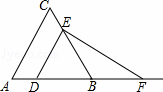
如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
如图①,②,③,用一种大小相等的正多边形密铺成一个“环”,我们称之为环形密铺.但图④,⑤不是我们所说的环形密铺.请你再写出一种可以进行环形密铺的正多边形: .

查看答案和解析>>
科目:初中数学 来源: 题型:
已 知函数
知函数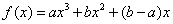 (a,b是不同时为零的常数),其导函数为
(a,b是不同时为零的常数),其导函数为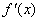 .
.
(1)当 时,若不等式
时,若不等式 对任意
对任意
 恒成立,求b的取值范围;
恒成立,求b的取值范围;
(2)若函数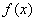 为奇函数,且在
为奇函数,且在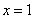 处的切线垂直于直线
处的切线垂直于直线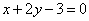 ,关于x的方程
,关于x的方程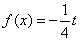 在
在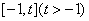 上有且只有一个实数根,求实数t的取值范围.
上有且只有一个实数根,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com