
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,△ABP和△DCE全等.
A. 1 B. 1或3 C. 1或7 D. 3或7
科目:初中数学 来源: 题型:
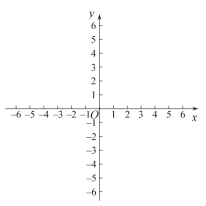
【题目】平面直角坐标系 xOy 中,抛物线 y = kx 2 - 2k 2 x -3 交 y 轴于 A 点,交直线 x=-4 于 B 点.
(1)抛物线的对称轴为直线 x=______(用含 k 的代数式表示);
(2)若 AB // x 轴,求抛物线的解析式;
(3)当-4<k<0时,记抛物线在 A,B 之间的部分为图象 G(包含 A,B 两点),若对于图象 G 上任意一点 P( xP , yP ), yP ≥-3 ,结合函数图象写出 k 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第20届世界杯足球赛正在如火如荼的进行,爸爸想通过一个游戏决定小明能否看今晚的比赛:在一个不透明的盒子中放入三张卡片,每张卡片上写着一个实数,分别为3,![]() , 2
, 2![]() (每张卡片除了上面的实数不同以外其余均相同),爸爸让小明从中任意取一张卡片,如果抽到的卡片上的数是有理数,就让小明看比赛,否则就不能看.
(每张卡片除了上面的实数不同以外其余均相同),爸爸让小明从中任意取一张卡片,如果抽到的卡片上的数是有理数,就让小明看比赛,否则就不能看.
(1)请你直接写出按照爸爸的规则小明能看比赛的概率;
(2)小明想了想,和爸爸重新约定游戏规则:自己从盒子中随机抽取两次,每次抽取一张卡片,第一次抽取后记下卡片上的数,再将卡片放回盒中抽取第二次,如果抽取的两数之积是有理数,自己就看比赛,否则就不看.请你用列表法或树状图法求出按照此规则小明看比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七![]() 班共有45人,该班计划为每名学生购买一套学具,超市现有A、B两种品牌学具可供选择
班共有45人,该班计划为每名学生购买一套学具,超市现有A、B两种品牌学具可供选择![]() 已知1套A学具和1套B学具的售价为45元;2套A学具和5套B学具的售价为150元.
已知1套A学具和1套B学具的售价为45元;2套A学具和5套B学具的售价为150元.
![]() 、B两种学具每套的售价分别是多少元?
、B两种学具每套的售价分别是多少元?
![]() 现在商店规定,若一次性购买A型学具超过20套,则超出部分按原价的6折出售
现在商店规定,若一次性购买A型学具超过20套,则超出部分按原价的6折出售![]() 设购买A型学具a套
设购买A型学具a套![]() 且不超过30套,购买A、B两种型号的学具共花费w元.
且不超过30套,购买A、B两种型号的学具共花费w元.
![]() 请写出w与a的函数关系式;
请写出w与a的函数关系式;
![]() 请帮忙设计最省钱的购买方案,并求出所需费用.
请帮忙设计最省钱的购买方案,并求出所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=3x﹣3分别交x轴,y轴于A,B两点,抛物线y=x2+bx+c经过A,B两点,点C是抛物线与x轴的另一个交点(与A点不重合)
(1)求抛物线的解析式:
(2)在抛物线的对称轴上是否存在点M,使△ABM周长最短?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式;
(2)求出四边形ABPC的面积最大时的P点坐标和四边形ABPC的最大面积;
(3)在直线BC找一点Q,使得△QOC为等腰三角形,写出Q点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在边长为3的等边![]() 中,点
中,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 方向运动,速度为1个单位/秒,同时点
方向运动,速度为1个单位/秒,同时点![]() 从点
从点![]() 出发,以相同的速度沿射线
出发,以相同的速度沿射线![]() 方向运动,过点
方向运动,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() 交射线
交射线![]() 于点
于点![]() .
.
(1)如图1,当![]() 时,求运动了多长时间?
时,求运动了多长时间?
(2)如图1,当点![]() 在线段
在线段![]() (不考虑端点)上运动时,是否始终有
(不考虑端点)上运动时,是否始终有![]() ?请说明理由;
?请说明理由;
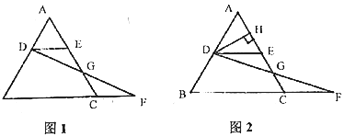
(3)如图2,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,当点
,当点![]() 在线段
在线段![]() (不考虑端点)上时,
(不考虑端点)上时,![]() 的长始终等于
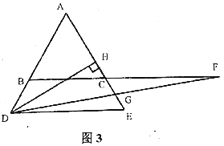
的长始终等于![]() 的一半;如图3,当点
的一半;如图3,当点![]() 运动到
运动到![]() 的延长线上时,
的延长线上时,![]() 的长是否发生变化?若改变,请说明理由;若不变,求出
的长是否发生变化?若改变,请说明理由;若不变,求出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点(不与点
上一点(不与点![]() 、点
、点![]() 重合),
重合),![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)请猜想![]() 与
与![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(2)若点![]() 为边
为边![]() 延长线上一点,
延长线上一点,![]() ,垂足为
,垂足为![]() ,交
,交![]() 延长线于点
延长线于点![]() ,请在图2中画出图形,并判断(1)中的结论是否成立.若成立,请证明;若不成立,请写出你的猜想并证明.
,请在图2中画出图形,并判断(1)中的结论是否成立.若成立,请证明;若不成立,请写出你的猜想并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学现有学生2650人,学校为了进一步了解学生课余生活,组织调查各兴趣小组活动情况,为此校学生会进行了一次随机抽样调查,根据采集到的数据,绘制如下两个统计图(不完整)
请你根据两个统计图中提供的信息,解答下列问题:
(1)这次抽样调查的样本容量是多少?在图2中,请将条形统计图中的“体育”部分的图形补充完整;
(2)爱好“书画”的人数占被调查人数的百分数是多少?估计该中学现有的学生中,爱好“书画”的人数;
(3)求爱好“音乐”的人数对应扇形圆心角的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com