【题目】如图，一次函数y=kx+b与反比例函数y=的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA=OB．

（1）求一次函数y=kx+b和y=的表达式；

（2）已知点C在x轴上，且△ABC的面积是8，求此时点C的坐标；

（3）反比例函数y=（1≤x≤4）的图象记为曲线C1，将C1向右平移3个单位长度，得曲线C2，则C1平移至C2处所扫过的面积是_________．(直接写出答案)

参考答案：

【答案】（1），；（2）点C的坐标为或；（3）27.

【解析】试题分析：（1）由点A的坐标利用反比例函数图象上点的坐标特征即可求出a值，从而得出反比例函数解析式；由勾股定理得出OA的长度从而得出点B的坐标，由点A、B的坐标利用待定系数法即可求出直线AB的解析式；
（2）设点C的坐标为（m，0），令直线AB与x轴的交点为D，根据三角形的面积公式结合△ABC的面积是8，可得出关于m的含绝对值符号的一元一次方程，解方程即可得出m值，从而得出点C的坐标；
（3）设点E的横坐标为1，点F的横坐标为6，点M、N分别对应点E、F，根据反比例函数解析式以及平移的性质找出点E、F、M、N的坐标，根据EM∥FN，且EM=FN，可得出四边形EMNF为平行四边形，再根据平行四边形的面积公式求出平行四边形EMNF的面积S，根据平移的性质即可得出C1平移至C2处所扫过的面积正好为S．

试题解析：

（1）∵点A（4，3）在反比例函数y=的图象上，

∴a=4×3=12，

∴反比例函数解析式为y=；

∵OA==5，OA=OB，点B在y轴负半轴上，

∴点B（0，﹣5）．

把点A（4，3）、B（0，﹣5）代入y=kx+b中，

得： ，解得： ，

∴一次函数的解析式为y=2x﹣5．

（2）设点C的坐标为（m，0），令直线AB与x轴的交点为D，如图1所示．

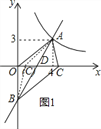
令y=2x﹣5中y=0，则x=，

∴D（，0），

∴S△ABC=CD（yA﹣yB）=|m﹣|×[3﹣（﹣5）]=8，

解得：m=或m=．

故当△ABC的面积是8时，点C的坐标为（，0）或（，0）．

（3）设点E的横坐标为1，点F的横坐为6，点M、N分别对应点E、F，如图2所示．

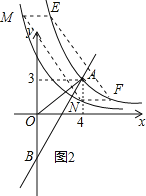
令y=中x=1，则y=12，

∴E（1，12），；

令y=中x=4，则y=3，

∴F（4，3），

∵EM∥FN，且EM=FN，

∴四边形EMNF为平行四边形，

∴S=EM（yE﹣yF）=3×（12﹣3）=27．

C1平移至C2处所扫过的面积正好为平行四边形EMNF的面积．

故答案为：27．

关闭