
【题目】如图,△ABC的三边AB、BC、CA长分别为30、40、50.其三条角平分线交于点O,则S△ABO :S△BCO :S△CAO =______ 。

 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点D、E分别在△ACD的边AB和AC上,已知DE∥BC,DE=DB.
(1)请用直尺和圆规在图中画出点D和点E(保留作图痕迹,不要求写作法),并证明所作的线段DE是符合题目要求的;
(2)若AB=7,BC=3,请求出DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小莉和她爸爸两人沿长江边扬子江步道匀速跑步,他们从渡江胜利纪念馆同时出发,终点是绿博园.已知小莉比她爸爸每步少跑![]() ,两人的运动手环记录时间和步数如下:
,两人的运动手环记录时间和步数如下:
出发 | 途中 | 结束 | |
时间 |
|
|
|
小莉的步数 | 1308 | 3183 | 8808 |
出发 | 途中 | 结束 | |
时间 |
|
|
|
爸爸的步数 | 2168 | 4168 |
|
(1)表格中![]() 表示的结束时间为 ,
表示的结束时间为 ,![]() ;
;
(2)小莉和她爸爸两人每步分别跑多少米?
(3)渡江胜利纪念馆到绿博园的路程是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
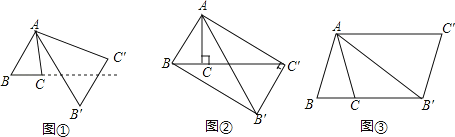
(1)如图①,对△ABC作变换[60°,![]() ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求一次函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C在x轴上,且△ABC的面积是8,求此时点C的坐标;
(3)反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)
(1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b)(m≠1且为实数),其中正确的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铜仁某校高中一年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球,共投10次.甲、乙两名同学测试情况如图所示:

![]() 根据图6提供的信息填写下表:
根据图6提供的信息填写下表:
平均数 | 众数 | 方差 | |
甲 |
| ||
乙 |
|
![]() 如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.
如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和爸爸周末到湿地公园进行锻炼,两人同时从家出发,匀速骑共享单车到达公园入口,然后一同匀速步行到达驿站,到达驿站后小明的爸爸立即又骑共享单车按照来时骑行速度原路返回,在公园入口处改为步行,并按来时步行速度原路回家,小明到达驿站后逗留了10分钟之后骑车回家,爸爸在锻炼过程中离出发地的路程与出发的时间的函数关系如图.
(1)图中m=_____,n=_____;(直接写出结果)
(2)小明若要在爸爸到家之前赶上,问小明回家骑行速度至少是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com