
【题目】小莉和她爸爸两人沿长江边扬子江步道匀速跑步,他们从渡江胜利纪念馆同时出发,终点是绿博园.已知小莉比她爸爸每步少跑![]() ,两人的运动手环记录时间和步数如下:
,两人的运动手环记录时间和步数如下:
出发 | 途中 | 结束 | |
时间 |
|
|
|
小莉的步数 | 1308 | 3183 | 8808 |
出发 | 途中 | 结束 | |
时间 |
|
|
|
爸爸的步数 | 2168 | 4168 |
|
(1)表格中![]() 表示的结束时间为 ,
表示的结束时间为 ,![]() ;
;
(2)小莉和她爸爸两人每步分别跑多少米?
(3)渡江胜利纪念馆到绿博园的路程是多少米?
【答案】(1)![]() ;7168;(2)小莉和她爸爸两人每步分别跑0.8米,1.2米;(3)渡江胜利纪念馆到绿博园的路程是6000米.
;7168;(2)小莉和她爸爸两人每步分别跑0.8米,1.2米;(3)渡江胜利纪念馆到绿博园的路程是6000米.
【解析】
(1)分别根据小莉和爸爸的出发到途中的时间变化和步数变化,求出每人速度,再根据途中和结束的时间内步数变化求出时间,最后确定两人结束的时间;
(2)由总路程等于步数乘以每步的长度,根据两人路程相等列方程求解;
(3)根据爸爸的步数乘以每步的长度计算总路程即可.
解:根据题意得小莉的速度为![]() =187.5步/分,
=187.5步/分,
∴途中到结束所用时间为![]() 分 ,
分 ,
∴a=7:40;
爸爸的速度为![]() 步/分,
步/分,
∴途中到结束所走的步数为![]() 步 ,
步 ,
∴b=4168+3000=7168步;
(2)设小莉的每步跑xm,根据题意得,
(8808-1308)x=(7168-2168)(x+0.4)
解得,x=0.8,
x+0.8=1.2m.
答:小莉和她爸爸两人每步分别跑0.8米,1.2米;
(3)(7168-2168) ×1.2=6000米
答:渡江胜利纪念馆到绿博园的路程是6000米.


科目:初中数学 来源: 题型:
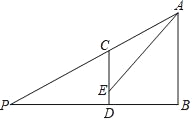
【题目】如图,某学校教学楼AB的后面有一建筑物CD,在距离CD正后方28米的观测点P处,以22°的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A,而在建筑物CD上距离地面2米高的E处,测得教学楼的顶端A的仰角为45°,求教学楼AB的高度(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
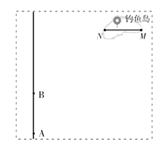
【题目】钓鱼岛自古就是中国的领土,我国有 关部门已对钓鱼岛及其附属岛屿开展常态化监视监测. M、N 为钓鱼岛上东西海岸线上的两点,MN 之间的距 离约为3.6km. 某日,我国一艘海监船从 A 点沿正北方 向巡航,在 A 点测得岛屿的西端点 N 在点 A 的北偏东350方向;海监船继续航行 4km 后到达 B 点 ,测得岛屿的东端点 M 在点 B 的北偏东 600方向,求点 M 距离海监船航线的最短距离 (结果精确到 0.1km).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)四边形ABCD中,已知∠ABC+∠ADC=180°,AB=AD,DA⊥AB,点E在CD的延长线上,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)求证:CA平分∠BCD;
(3)如图(2),设AF是△ABC的BC边上的高,求证:EC=2AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了美化环境,计划在一定的时间内完成绿化面积![]() 万亩的任务,后来市政府调整了原定计划,不但绿化面积要在原计划的基础上增加
万亩的任务,后来市政府调整了原定计划,不但绿化面积要在原计划的基础上增加![]() ,而且要提前
,而且要提前![]() 年完成任务,经测算要完成新的计划,平均每年的绿化面积必须比原计划多
年完成任务,经测算要完成新的计划,平均每年的绿化面积必须比原计划多![]() 万亩,求原计划平均每年的绿化面积.
万亩,求原计划平均每年的绿化面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,点E是CD上的点(不与CD的中点重合), DE=AB, ∠BAC=∠D,AD=AC

(1)求证:四边形AECB是等腰梯形;
(2)点F 是AB 边延长线上一点,且BC=CF .联结CF、EF,若AC⊥EF求证:四边形AECF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是![]() 和
和![]() ,若CD的长是点C到海平面的最短距离.
,若CD的长是点C到海平面的最短距离.
![]() 问BD与AB有什么数量关系,试说明理由;
问BD与AB有什么数量关系,试说明理由;
![]() 求信号发射点的深度
求信号发射点的深度![]() 结果精确到1m,参考数据:
结果精确到1m,参考数据:![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )

A. 2B. 2.2C. 2.4D. 2.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com