
【题目】已知点C是线段AB上一点,在线段AB的同侧作△CAD和△CBE,直线BD和AE相交于点F,CA=CD,CB=CE,∠ACD=∠BCE。


(1)如图①,若∠ACD=600,则∠AFB=___________;若∠ACD=![]() ,则∠AFB=___________。
,则∠AFB=___________。
(2)如图②,将图①中的△CAD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),试探究∠AFB与![]() 的数量关系,并说明理由。
的数量关系,并说明理由。
【答案】(1)120°;180°![]() ;(2) ∠AFB=180°
;(2) ∠AFB=180°![]() .
.
【解析】
(1)由∠ACD=∠BCE得到∠ACE=∠DCB,通过证明△ACE≌△DCB得∠CBD=∠CEA,由三角形内角和定理得到结论∠AFB=180°-![]() ,代入∠ACD=60°即可求解.
,代入∠ACD=60°即可求解.
(2)由∠ACD=∠BCE得到∠ACE=∠DCB,再由三角形的内角和定理得∠CAE=∠CDB,从而得出∠DFA=∠ACD,得到结论∠AFB=180°-![]() .
.
(1)∵∠ACD=∠BCE=![]() ,则∠ACD+∠DCE=∠BCE+∠DCE,
,则∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB.
在△ACE和△DCB中 ,
,
则△ACE≌△DCB(SAS).
则∠CBD=∠CEA,由三角形内角和知∠EFB=∠ECB=![]() .
.
∠AFB=180°∠EFB=180°![]() .
.
故当∠ACD=60°,∠AFB=180°60°=120°
故答案为:120°;180°![]() ;
;
(2)∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE.
∴∠ACE=∠DCB.
∴∠CAE=∠CDB.
∴∠DFA=∠ACD.
∴∠AFB=180°∠DFA=180°∠ACD=180°![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,∠MON=45°,P为∠MON内一点,A为OM上一点,B为ON上一点,当![]() PAB的周长取最小值时,∠APB的度数为( )
PAB的周长取最小值时,∠APB的度数为( )

A.80°B.90°C.110°D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线![]() 过点B,C.
过点B,C.
(1)求b、c的值;
(2)若点D是抛物线在x轴下方图象上的动点,过点D作x轴的垂线,与直线BC相交于点E.当线段DE的长度最大时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划一次性购买排球和篮球,每个篮球的价格比排球贵30元;购买2个排球和3个篮球共需340元.
(1)求每个排球和篮球的价格:
(2)若该校一次性购买排球和篮球共60个,总费用不超过3800元,且购买排球的个数少于39个.设排球的个数为m,总费用为y元.
①求y关于m的函数关系式,并求m可取的所有值;
②在学校按怎样的方案购买时,费用最低?最低费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D、E分别在△ACD的边AB和AC上,已知DE∥BC,DE=DB.
(1)请用直尺和圆规在图中画出点D和点E(保留作图痕迹,不要求写作法),并证明所作的线段DE是符合题目要求的;
(2)若AB=7,BC=3,请求出DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,

求证:(1)∠BGC=90°+![]() ∠BAC;
∠BAC;
(2)∠1=∠2.
查看答案和解析>>
科目:初中数学 来源: 题型:
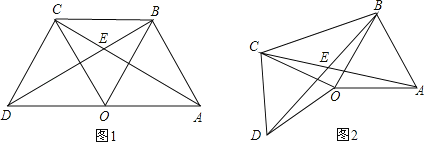
【题目】(1)如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小;
(2)如图2,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕点O旋转(△OAB和△OCD不能重叠),求∠AEB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求一次函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C在x轴上,且△ABC的面积是8,求此时点C的坐标;
(3)反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)
(1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com