
����Ŀ����ͼ����֪���κ��� y��ax2+![]() x+c ��ͼ���� y �ύ�ڵ� A��0��4����
x+c ��ͼ���� y �ύ�ڵ� A��0��4����
�� x �ύ�ڵ� B��C���� C ����Ϊ��8��0�������� AB��AC��
��1����ֱ��д�����κ��� y��ax2+![]() x+c �ı���ʽ��
x+c �ı���ʽ��
��2���ж���ABC ����״����˵�����ɣ�
��3������ N �� x �����˶������Ե� A��N��C Ϊ������������ǵ���������ʱ�� ��ֱ��д����ʱ�� N �����ꣻ
��4������ N ���߶� BC ���˶�������� B��C �غ��������� N �� NM��AC����AB �ڵ� M������AMN ������ʱ�����ʱ�� N �����꣮
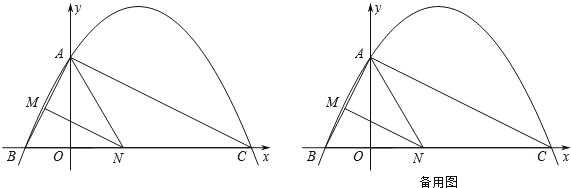
���𰸡���1��y����![]() x2+
x2+![]() x+4����2����ABC��ֱ�������Σ����ɼ���������3����N������ֱ�Ϊ����8��0������8��4
x+4����2����ABC��ֱ�������Σ����ɼ���������3����N������ֱ�Ϊ����8��0������8��4![]() ��0������3��0������8+4
��0������3��0������8+4![]() ��0������4������AMN������ʱ��N������Ϊ��3��0����
��0������4������AMN������ʱ��N������Ϊ��3��0����
��������
��1�����ô���ϵ������⼴�ɣ�
��2�������AB��AC��BC�ij���Ȼ����ݹ��ɶ������涨������֤�á�ABCΪֱ����������
��3���ֱ���A��C����ΪԲ�ģ�AC��Ϊ�뾶��������x�ύ�������㣬��AC�Ĵ�ֱƽ������x�ύ��һ���㣬�ֱ���õ�N�����꼴�ɣ�
��4�����N������Ϊ��n��0������BN��n+2����M����MD��x���ڵ�D���������������ƶ�Ӧ�߳ɱ������MD��![]() ��n+2����Ȼ�����S��AMN��S��ABN��S��BMN�ó�����n�Ķ��κ��������ݺ�������ʽ��ü���.
��n+2����Ȼ�����S��AMN��S��ABN��S��BMN�ó�����n�Ķ��κ��������ݺ�������ʽ��ü���.
������1�������κ���y��ax2+![]() x+c��ͼ����y�ύ�ڵ�A��0��4������x�ύ�ڵ�B��C����C����Ϊ��8��0����
x+c��ͼ����y�ύ�ڵ�A��0��4������x�ύ�ڵ�B��C����C����Ϊ��8��0����
![]() ��
��
���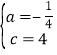 ��
��
�������߱���ʽ��y����![]() x2+
x2+![]() x+4��
x+4��
��2����ABC��ֱ�������Σ�
�� y��0������![]() x2+
x2+![]() x+4��0�� ��� x1��8��x2����2��
x+4��0�� ��� x1��8��x2����2��
���� B ����������2��0����
����֪�ɵã�
��Rt�� ABO����AB2��BO2+AO2��22+42��20��
��Rt��AOC����AC2��AO2+CO2��42+82��80��
����BC��OB+OC��2+8��10��
������ABC����AB2+AC2��20+80��102��BC2��
���ABC ��ֱ����������
��3����A��0��4����C��8��0����
��AC��![]() ��4
��4![]() ��
��
����AΪԲ�ģ���AC��Ϊ�뾶��Բ���� x ���� N����ʱ N ������Ϊ����8��0����
����CΪԲ������AC��Ϊ�뾶��Բ����x����N����ʱN������Ϊ��8��4![]() ��0����8+4
��0����8+4 ![]() ��0����
��0����
����AC�Ĵ�ֱƽ���ߣ���x����N����ʱN������Ϊ��3��0����
���ϣ�����N��x�����˶������Ե�A��N��CΪ������������ǵ���������ʱ�� ��N������ֱ�Ϊ����8��0������8��4![]() ��0������3��0������8+4
��0������3��0������8+4![]() ��0����
��0����
��4�����N������Ϊ��n��0������BN��n+2����M����MD��x���ڵ�D��
��MD��OA��
���BMD�ס�BAO��
��![]() ��
��
��MN��AC��
��![]() ��
��
��![]() ��
��
��AO��4��BC��10��BN��n+2��
��MD��![]() ��n+2����
��n+2����
��S��AMN��S��ABN��S��BMN��
��![]() BNOA��
BNOA��![]() BNMD
BNMD
��![]() ��n+2����4��
��n+2����4��![]() ��
��![]() ��n+2��2
��n+2��2
����![]() ��n��3��2+5��
��n��3��2+5��
������AMN ������ʱ��N������Ϊ��3��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�![]() Ϊԭ�㣬��ֱ֪��
Ϊԭ�㣬��ֱ֪��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ���
���![]() ����
����![]() ��Գƣ���ͼ�٣�
��Գƣ���ͼ�٣�
��1����![]() ������Ϊ________����
������Ϊ________����![]() ������Ϊ________����
������Ϊ________����![]() ������Ϊ________��ֱ��
������Ϊ________��ֱ��![]() �Ľ���ʽΪ________��
�Ľ���ʽΪ________��
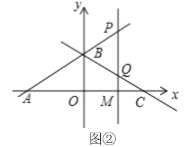
��2����![]() ��
��![]() ���ϵ�һ�����㣨��
���ϵ�һ�����㣨��![]() �����
�����![]() �غϣ�������
�غϣ�������![]() ��
��![]() ��Ĵ��ߣ���ֱ��
��Ĵ��ߣ���ֱ��![]() �ڵ�
�ڵ�![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ��ͼ�ڣ���
��ͼ�ڣ���
����ͼ�ڣ�����![]() ��
��![]() �����������ʱ����
�����������ʱ����![]() �����Ϊ
�����Ϊ![]() �����
�����![]() �����ꣻ
�����ꣻ
������![]() ����
����![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ڱ�ֱ�ĵ�·AB��������У��������г���A�ص�B�أ��Ҽݳ���B�ص�A�أ��������Ƿֱ��Բ�ͬ���ٶ�������ʻ�����ȳ���6���Ӻ��Ҳų����������������У��ס�������֮��ľ���y��ǧ�ף���׳�����ʱ��x���֣�֮��ĺ���ͼ����ͼ��
��1��A����B�����______km�����ٶ�Ϊ______km/�֣�
��2����ס�����������ʱ������ʻ��·�̣�
��3�����ҵ����յ�Aʱ��������ٷ��ӵ����յ�B��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����н�����̣�
 =
= =
=![]() =
=![]() -2��
-2��
 =
= =
=![]() ��
��
��ش��������⣺
��1���۲�����Ľ�����̣���ֱ��д��ʽ��![]() =�� ����
=�� ����
��2���۲�����Ľ�����̣���ֱ��д��ʽ��![]() =�� ����
=�� ����
��3�������������ṩ�Ľⷨ������![]() +������+
+������+![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() �����������ֱ�Ϊ
�����������ֱ�Ϊ![]()
![]()

��1������![]() ����ԭ��
����ԭ��![]() �����ĶԳƵ�
�����ĶԳƵ�![]() ��
��
��2��������![]() ����
����![]() ��ĶԳƵ�
��ĶԳƵ�![]() ���ѵ�
���ѵ�![]() ����ƽ��
����ƽ��![]() ����λ���Ⱥ�����
����λ���Ⱥ�����![]() ���ڲ�������������ͱ߽磩��
���ڲ�������������ͱ߽磩��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��������
��������![]() ʱ������������ͼ�����
ʱ������������ͼ�����![]() �������㣬��
�������㣬��![]() �����������( )
�����������( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD,��EΪAB���е�,��BF=![]() BC.
BC.
��1����ͼ1����֤��DE��EF.
��2����ͼ2������G��BC�ϣ���CD=3CG��DG��EF����H�㣬��![]() ��ֵ.
��ֵ.

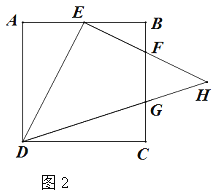
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��һ�ҵ��Ӽ�����ר����IJ�Ʒÿ������13Ԫ,�ۼ�20Ԫ,�����Żݡ�����һ����10�����ϵ�,ÿ����1��,�����ȫ��������ÿ���ͽ���0.10Ԫ.����,ij����20��������,����ÿ������0.10��(20-10)=1(Ԫ),��������ȫ��20��������������ÿ��19Ԫ���㡣������ͼ�Ϊÿ��16Ԫ��
(1)д����ר���굱һ������x��ʱ,��������y(Ԫ)��x(��)֮��ĺ�������ʽ,��д���Ա���x��ȡֵ��Χ��
(2)������һ�����ĸ�����10��50��֮��,��:һ�������ٸ���õ��������?���������Ϊ����?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com