
【题目】如图:BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H.∠GFH+∠BHC=180°,求证:∠1=∠2. 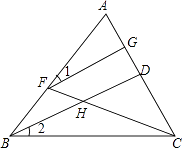
科目:初中数学 来源: 题型:
【题目】某校四个绿化小组一天植树的棵数如下:10,x,10,8.已知这组数据的众数与平均数相等,则这组数据的中位数是( )
A. 8 B. 9 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下: 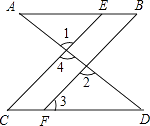
∵∠1=∠2(),
且∠1=∠4()
∴∠2=∠4(等量代换)
∴CE∥BF()
∴∠=∠3()
又∵∠B=∠C(已知)
∴∠3=∠B()
∴AB∥CD().
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个.比赛结束后随机抽查部分学生听写结果,图1,图2是根据抽查结果绘制的统计图的一部分.
组别 | 听写正确的个数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
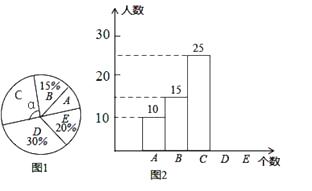
根据以上信息解决下列问题:
(1)本次共随机抽查了多少名学生,求出m,n的值并补全图2的条形统计图;
(2)求出图1中∠α的度数;
(3)该校共有3000名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料: 解分式不等式 ![]() .
.
解:根据实数的除法法则,同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为:
① ![]() ,②
,② ![]() .
.
解不等式组①,得:x>3.
解不等式组②,得:x<﹣2.
所以原分式不等式的解集是x>3或x<﹣2.
请仿照上述方法解分式不等式: ![]() <0.
<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com