
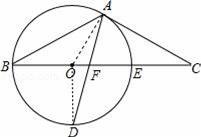
如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
(1)求证:AC是⊙O的切线:
(2)若BF=8,DF=
 ,求⊙O的半径r.
,求⊙O的半径r.


【考点】切线的判定.
【分析】(1)连接OA、OD,求出∠D+∠OFD=90°,推出∠CAF=∠CFA,∠OAD=∠D,求出∠OAD+∠CAF=90°,根据切线的判定推出即可;
(2)OD=r,OF=8﹣r,在Rt△DOF中根据勾股定理得出方程r2+(8﹣r)2=(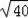
 )2,求出即可.
)2,求出即可.
【解答】(1)证明:
连接OA、OD,
∵D为弧BE的中点,
∴OD⊥BC,
∠DOF=90°,
∴∠D+∠OFD=90°,
∵AC=FC,OA=OD,
∴∠CAF=∠CFA,∠OAD=∠D,
∵∠CFA=∠OFD,
∴∠OAD+∠CAF=90°,
∴OA⊥AC,
∵OA为半径,
∴AC是⊙O切线;
(2)解:∵⊙O半径是r,
∴OD=r,OF=8﹣r,
在Rt△DOF中,r2+(8﹣r)2=(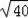
 )2,
)2,
r=6,r=2(舍),当r=2时,OB=OE=2,OF=BF﹣OB=8﹣2=6>OE,∴y舍去;
即⊙O的半径r为6.,

【点评】本题考查了切线的判定,等腰三角形的性质和判定,勾股定理等知识点的应用,主要考查学生的推理和计算的能力.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
如图,已知E(﹣4,2),F(﹣1,﹣1),以原点O为位似中心,按比例尺2:1把△EFO缩小,则E点对应点E′的坐标为( )


A.(2,1) B.(
 ,
,
 ) C.(2,﹣1) D.(2,﹣
) C.(2,﹣1) D.(2,﹣
 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
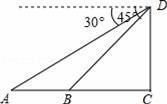
如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A、B、C在同一条直线上),则河的宽度AB约是多少m?(精确到0.1m).(参考数据: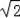
 ≈1.41,
≈1.41,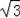
 ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
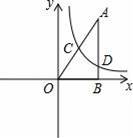
如图,Rt△ABO在直角坐标系中,AB⊥x轴于点B,AO=10,sin∠AOB=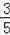
 ,反比例函数y=
,反比例函数y=
 (x>0)的图象经过AO的中点C,且与AB交于点D,则BD= .
(x>0)的图象经过AO的中点C,且与AB交于点D,则BD= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com