
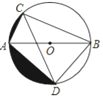
【题目】如图,AB为⊙O的直径,弦AC=2,∠ABC=30°,∠ACB的平分线交⊙O于点D,求:
(1)BC、AD的长;
(2)图中两阴影部分面积的和.
【答案】(1)2![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据直径得出∠ACB=∠ADB=90°,根据勾股定理求出BC,根据圆周角定理求出AD=BD,求出AD即可;
(2)根据三角形的面积公式,求出△AOC和△AOD的面积,再求出S扇形COD,即可求出答案.
解:(1)∵AB是直径,
∴∠ACB=∠ADB=90°(直径所对的圆周角是直角),
在Rt△ABC中,∠ABC=30°,AC=2,
∴AB=4,
∴BC=![]() ,
,
∵∠ACB的平分线交⊙O于点D,
∴∠DCA=∠BCD
∴![]() ,
,
∴AD=BD,
∴在Rt△ABD中,AD=BD=![]() AB=2
AB=2![]() ;
;
(2)连接OC,OD,
∵∠ABC=30°,
∴∠AOC=∠2∠ABC=60°,
∵OA=OB,
∴S△AOC=![]() S△ABC=
S△ABC=![]() ×
×![]() ×AC×BC=
×AC×BC=![]() ×
×![]() ×2×2
×2×2![]() =
=![]() ,
,
由(1)得∠AOD=90°,
∴∠COD=150°,
S△AOD=![]() ×AO×OD=
×AO×OD=![]() ×22=2,
×22=2,
∴S阴影=S扇形COD﹣S△AOC﹣S△AOD=![]() ﹣
﹣![]() ﹣2=
﹣2=![]() π﹣
π﹣![]() ﹣2.
﹣2.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:初中数学 来源: 题型:
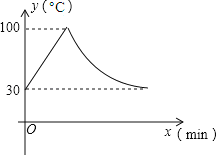
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的
A.7:20 B.7:30 C.7:45 D.7:50
查看答案和解析>>
科目:初中数学 来源: 题型:
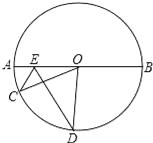
【题目】如图,点E为⊙O的直径AB上一个动点,点C、D在下半圆AB上(不含A、B两点),且∠CED=∠OED=60°,连OC、OD
(1)求证:∠C=∠D;
(2)若⊙O的半径为r,请直接写出CE+ED的变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
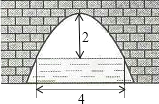
【题目】如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )
A.3 B.2![]() C.3
C.3![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
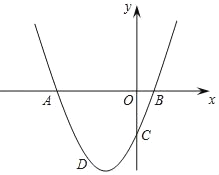
【题目】已知,抛物线y=ax2+2ax+c与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)当a>0时,如图所示,若点D是第三象限方抛物线上的动点,设点D的横坐标为m,三角形ADC的面积为S,求出S与m的函数关系式,并直接写出自变量m的取值范围;请问当m为何值时,S有最大值?最大值是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
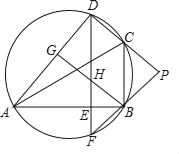
【题目】如图,D是△ABC外接圆上的点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:∠BAD=∠PCB;
(2)求证:BG∥CD;
(3)设△ABC外接圆的圆心为O,若AB=![]() DH,∠COD=23°,求∠P的度数.
DH,∠COD=23°,求∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一个由小正方体组成的几何体的左视图和俯视图.

![]() 该几何体最少需要几块小正方体?最多可以有几块小正方体?
该几何体最少需要几块小正方体?最多可以有几块小正方体?
![]() 请画出该几何体的所有可能的主视图.
请画出该几何体的所有可能的主视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=5,BC=3.
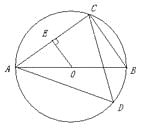
(1) 求sin∠BAC的值;
(2) 如果OE⊥AC, 垂足为E,求OE的长;
(3) 求tan∠ADC的值.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是△ABC的内心,线段AE的延长线交△ABC的外接圆于点D.
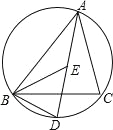
(1)求证:ED=BD;
(2)若∠BAC=90°,△ABC的外接圆的直径是6,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com