
【题目】如图,点E是△ABC的内心,线段AE的延长线交△ABC的外接圆于点D.
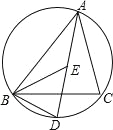
(1)求证:ED=BD;
(2)若∠BAC=90°,△ABC的外接圆的直径是6,求BD的长.
【答案】(1)证明见解析;(2)3![]() .
.
【解析】
试题分析:(1)根据点E是△ABC的内心得出∠BAD=∠CAD,∠ABE=∠CBE,求出∠BED=∠EBD,即可得出答案;
(2)求出BC为△ABC的直径,求出BD=DC,解直角三角形求出即可.
试题解析:(1)∵点E是△ABC的内心,
∴∠BAD=∠CAD,∠ABE=∠CBE,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∴∠BED=∠ABE+∠BAD,
∴∠ABE=∠CBE,∠BAD=∠CAD=∠CBD,
∵∠EBD=∠CBE+∠CBD,
∴∠BED=∠EBD,
∴ED=BD;
(2)连接CD,
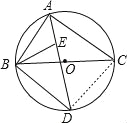
∵∠BAC=90°,
∴BC是⊙O的直径,
∴∠BDC=90°,
∵⊙O的直径=6,
∴BC=6,
∵E为△ABC的内切圆的圆心,
∴∠BAD=∠CAD,
∴BD=DC,
∴BD=DC=![]() BC=3
BC=3![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
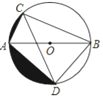
【题目】如图,AB为⊙O的直径,弦AC=2,∠ABC=30°,∠ACB的平分线交⊙O于点D,求:
(1)BC、AD的长;
(2)图中两阴影部分面积的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
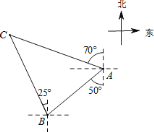
【题目】如图,轮船在![]() 处观测灯塔
处观测灯塔![]() 位于北偏西
位于北偏西![]() 方向上,轮船从
方向上,轮船从![]() 处以每小时
处以每小时![]() 海里的速度沿南偏西
海里的速度沿南偏西![]() 方向匀速航行,
方向匀速航行,![]() 小时后到达码头
小时后到达码头![]() 处,此时,观测灯塔
处,此时,观测灯塔![]() 位于北偏西
位于北偏西![]() 方向上,则灯塔
方向上,则灯塔![]() 与码头
与码头![]() 的距离是____海里.(结果精确到个位,参考数据:
的距离是____海里.(结果精确到个位,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1 , 依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018 , 如果点A的坐标为(![]() ,0),那么点B2018的坐标为( )
,0),那么点B2018的坐标为( )

A. (1,1) B. (0,![]() ) C. (﹣1,1) D. (-
) C. (﹣1,1) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一款进价为每件40元的护肤品,调查发现,销售单价不低于40元且不高于80元时,该商品的日销售量y(件)与销售单价x(元)之间存在一次函数关系,当销售单价为44元时,日销售量为72件;当销售单价为48元时,日销售量为64件.
(1)求y与x之间的函数关系式;
(2)设该护肤品的日销售利润为w(元),当销售单价x为多少时,日销售利润w最大,最大日销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
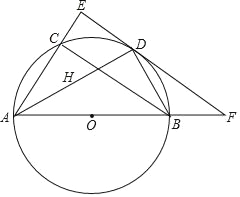
【题目】如图,在直角三角形ABC中,∠ACB=90°,点H是△ABC的内心,AH的延长线和三角形ABC的外接圆O相交于点D,连结DB.
(1)求证:DH=DB;
(2)过点D作BC的平行线交AC、AB的延长线分别于点E、F,已知CE=1,圆O的直径为5.
①求证:EF为圆O的切线;
②求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
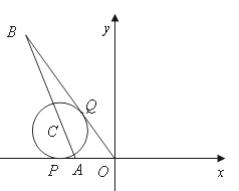
【题目】如图,直线y=-2x-10与x轴交于点A,直线y=-![]() x交于点B,点C在线段AB上,⊙C与x轴相切于点P,与OB切于点Q.求:(1)A点的坐标;(2)OB的长;(3)C点的坐标.
x交于点B,点C在线段AB上,⊙C与x轴相切于点P,与OB切于点Q.求:(1)A点的坐标;(2)OB的长;(3)C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
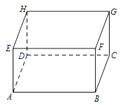
【题目】如图 所示,一个长方体的长、宽、高分别是 ![]() ,
,![]() ,
,![]() ,有一只蚂蚁从点
,有一只蚂蚁从点 ![]() 出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点
出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点 ![]() 时,最多爬行多远?并把蚂蚁所爬行的路线用字母按顺序表示出来.
时,最多爬行多远?并把蚂蚁所爬行的路线用字母按顺序表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
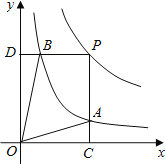
【题目】函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=![]() AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com