
【题目】(如图(1),在矩形ABCD中,AB=4,BC=3,点E是射线CD上的一个动点,把△BCE沿BE折叠,点C的对应点为F.
(1)若点F刚好落在线段AD的垂直平分线上时,求线段CE的长;
(2)若点F刚好落在线段AB的垂直平分线上时,求线段CE的长;
(3)当射线AF交线段CD于点G时,请直接写出CG的最大值 .


【答案】(1)CE=![]() ;(2)CE=
;(2)CE=![]() ;(3)CG的最大值是4-
;(3)CG的最大值是4-![]()
【解析】(1)根据垂直平分线的性质,等边三角形的性质求出即可;(2)利用垂直平分线的性质得出FE=EC ,再利用相似三角形的性质进而得出答案;(3)当射线AF交线段CD于点G时求出即可.
解: ∵点F刚好落在线段AD的垂直平分线上,∴FB=FC.
∵折叠 ,∴FB=BC=3.
∴△FBC是等边三角形,∴∠FBC=60°, ∠EBC=30°.
在Rt△EBC,∴CE=![]() BC=
BC=![]() .
.
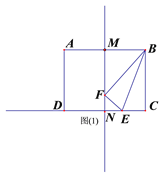
(2)如图(1)∵点F刚好落在线段AB的垂直平分线MN上,
∵折叠,∴FE=EC.
∴BM=2,在Rt△MFB中,MF=![]() .
.
∵△MBF∽△NFE,
∴![]() =
=![]() .
.
∴CE=EN=![]() .
.
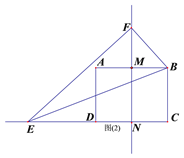
如图(2)∵折叠 ,∴FE=EC.
同理MF=![]() ,FN=3+
,FN=3+![]() .
.
∵△MBF∽△NFE,∴![]() =
=![]() .
.
∴CE=EN=![]() .
.
(3)CG的最大值是4-![]() .
.
“点睛”此题主要考查了垂直平分线、等边三角形、矩形的性质、翻折变换的性质、相似三角形等知识;利用数形结合以及分类讨论得出是解题关键.


科目:初中数学 来源: 题型:
【题目】如图,小敏家厨房一墙角处有一自来水管,装修时为了美观,准备用木板从AB处将水管密封起来,互相垂直的两墙面与水管分别相切于D,E两点,经测量AD=10cm,BE=15cm, 则该自来水管的半径为( )cm.
A.5
B.10
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
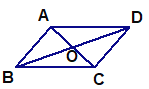
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,其中AC+BD=14,CD=5.
(1)若四边形ABCD是平行四边形,则△OCD的周长为_____________;
(2) 若四边形ABCD是矩形,则AD的长为_____________;
(3) 若四边形ABCD是菱形,则菱形的面积为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股民李星星在上周星期五以每股 11.2 元买了一批股票,下表为本周星期一 到星期五该股票的涨跌情况

求:(1)本周星期三收盘时,每股的钱数.
(2)李星星本周内哪一天把股票抛出比较合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据给出的数轴及已知条件,解答下面的问题:
![]()
(1)已知点A,B,C表示的数分别为1,2.5,﹣3观察数轴,B,C两点之间的距离为 ;
与点A的距离为3的点表示的数是 ;
(2)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是 ;
若此数轴上M,N两点之间的距离为2015(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则M,N两点表示的数分别是:M: ,N: ;
(3)若数轴上P,Q两点间的距离为m(P在Q左侧),表示数n的点到P,Q两点的距离相等,则将数轴折叠,使得P点与Q点重合时,P,Q两点表示的数分别为:P: ,Q: (用含m,n的式子表示这两个数).
查看答案和解析>>
科目:初中数学 来源: 题型:
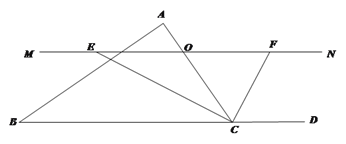
【题目】已知△ABC中,点O是边AC上的一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF.
(2)试确定点O在边AC上的位置,使四边形AECF是矩形,并加以证明.
(3)在(2)的条件下,且△ABC满足 ____________时,矩形AECF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中, E、F、G、H分别是边AB、BC、CD、DA的中点,若AC=BD,且EG2+FH2=16,则AC的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)45+(-22)+(-8)-(-5);(2)(-4![]() )-(-5
)-(-5![]() )+(-4
)+(-4![]() )-3
)-3![]() ;
;
(3)![]() ÷
÷![]() ; (4)-14+|3-5|-16÷(-2)×
; (4)-14+|3-5|-16÷(-2)×![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com