
【题目】如图,在四边形ABCD中, E、F、G、H分别是边AB、BC、CD、DA的中点,若AC=BD,且EG2+FH2=16,则AC的长为________.

【答案】4
【解析】分析:根据三角形的中位线定理和菱形的判定,可得顺次连接对角线相等的四边形各边中点所得四边形是菱形,根据菱形的性质得到EG⊥HF,再由勾股定理得出EH的长,从而得到答案.
详解:如图,设EG和FH相交于点O.
∵E、F、G、H分别是线段AB、BC、CD、AD的中点,∴EH、FG分别是△ABD、△BCD的中位线,EF、HG分别是△ACD、△ABC的中位线,根据三角形的中位线的性质知,EH=FG=![]() BD,EF=HG=
BD,EF=HG=![]() AC.
AC.
又∵AC=BD,∴EH=FG=EF=HG,∴四边形EFGH是菱形,∴EG⊥HF,EO=![]() EG,OH=
EG,OH=![]() HF,∴EF=EH=
HF,∴EF=EH=![]() =
=![]() =
=![]() =
=![]() =2,∴AC=2EF=4.
=2,∴AC=2EF=4.

故答案为:4.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】我们都知道无限不循环小数是无理数,而无限循环小数是可以化成分数的。例如![]() (3为循环节)是可以化成分数的,方法如下:
(3为循环节)是可以化成分数的,方法如下:
令![]() ①
①
则![]() ②
②
②-①得![]()
![]()
![]()
所以![]() 可以化成分数为
可以化成分数为![]()
请你阅读上面材料完成下列问题:
(1)![]() (
(![]() )化成分数是 .
)化成分数是 .
(2)请你将![]() (
(![]() )化为分数.
)化为分数.
(3)请你将![]() (
(![]() )化为分数.
)化为分数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(如图(1),在矩形ABCD中,AB=4,BC=3,点E是射线CD上的一个动点,把△BCE沿BE折叠,点C的对应点为F.
(1)若点F刚好落在线段AD的垂直平分线上时,求线段CE的长;
(2)若点F刚好落在线段AB的垂直平分线上时,求线段CE的长;
(3)当射线AF交线段CD于点G时,请直接写出CG的最大值 .


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的液体,并用流量、速度、密度三个概念描述车流的基本特征。其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度(辆/千米)指通过道路指定断面单位长度内的车辆数,为配合大数据治堵行动,测得某路段流量q与速度v之间的部分数据如下表:
速度v(千米/小时) | … | 5 | 10 | 20 | 32 | 40 | 48 | … |
流量q(辆/小时) | … | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | … |
(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是(只需填上正确答案的序号)① ![]() ②
② ![]() ③
③ ![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足 ![]() ,请结合(1)中选取的函数关系式继续解决下列问题:
,请结合(1)中选取的函数关系式继续解决下列问题:
①市交通运行监控平台显示,当 ![]() 时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)-5.4+0.2-0.6+1.8
(2) (-26.54)+(-6.4)+18.54+6.4
(3) ![]()
(4)![]()
(5)![]()
(6) ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A、B、C、D四个等级,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题:

(1)抽取了__名学生成绩;
(2)请把频数分布直方图补充完整;
(3)扇形统计图中A等级所在的扇形的圆心角度数是__;
(4)若A、B、C三个等级为合格,该校初二年级有900名学生,估计全年级生物合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
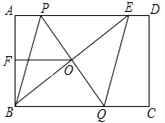
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF =4,求菱形BPEQ的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设x是正实数,我们用{x}表示不小于x的最小正整数,如{0.7}=1,{2}=2,{3.1}=4,在此规定下任一正实数都能写成如下形式:x={x}-m,其中O≤m<l.
(1)直接写出{x}与x,x+1的大小关系:
(2)根据(1)中的关系式,求满足{2x-1}=3的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为( )
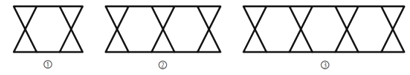
A. 12 B. 14 C. 16 D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com