
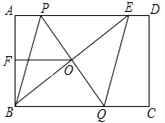
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF =4,求菱形BPEQ的周长.
【答案】(1)见解析;(2)25.
【解析】分析:(1)先根据线段垂直平分线的性质证明PB=PE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形ABGE是平行四边形,再根据菱形的判定即可得出结论;
(2)由三角形中位线定理得AE的长,设PE=y,则AP=8-y,BP=PE=y.在Rt△ABP中,由勾股定理可求得y的值,即可得到结论.
详解:(1)∵PQ垂直平分BE,∴QB=QE,OB=OE.
∵四边形ABCD是矩形,∴AD∥BC,∴∠PEO=∠QBO,
在△BOQ与△EOP中.
∵∠PEO=∠QBO,OB=OE,∠POE=∠QOB,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,∴四边形BPEQ是平行四边形,
又∵QB=QE,∴四边形BPEQ是菱形;
(2)∵O,F分别为PQ,AB的中点,OF=4 ∴AE=8,
设PE=y,则AP=8-y,BP=PE=y.在Rt△ABP中,62+(8-y)2=y2,解得:y=![]() ,
,
∴菱形BPEQ的周长=25.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
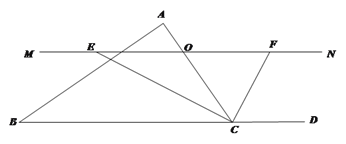
【题目】已知△ABC中,点O是边AC上的一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF.
(2)试确定点O在边AC上的位置,使四边形AECF是矩形,并加以证明.
(3)在(2)的条件下,且△ABC满足 ____________时,矩形AECF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中, E、F、G、H分别是边AB、BC、CD、DA的中点,若AC=BD,且EG2+FH2=16,则AC的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用火柴棒按下列方式搭三角形:

(1)填写下面表
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | … |
(2)搭10个这样的三角形需要 根火柴棒.
(3)搭n个这样的三角形需要 根火柴棒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,﹣ ![]() ,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn.
,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn.
(1)请用列表或画树状图的方法表示取出数字的所有结果;
(2)求正比例函数y=kx的图象经过第一、三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)45+(-22)+(-8)-(-5);(2)(-4![]() )-(-5
)-(-5![]() )+(-4
)+(-4![]() )-3
)-3![]() ;
;
(3)![]() ÷
÷![]() ; (4)-14+|3-5|-16÷(-2)×
; (4)-14+|3-5|-16÷(-2)×![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
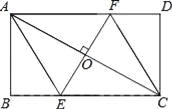
【题目】如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=![]() ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com