Question

【题目】如图，在同一个平面内，，.

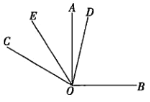
（1）填空：________；

（2）如果OD平分，OE平分，那么的度数为；

（3）试问在（2）的条件下，如果将题目中改为，其他条件不变，你能求出的度数吗？若能，请你写出求解过程；若不能，请说明理由.

Answer 1

【答案】（1）150°（2）45°（3）45°

【解析】

（1）直接根据已知利用∠BOC=∠AOB+∠AOC求出即可；

（2）利用角平分线的性质和（1）中所求得出答案即可；

（3）根据角平分线的性质∠DOC=∠BOC=45°+α，∠COE=∠AOC=α，进而求出即可．

(1)∵∠AOB=90°,∠AOC=60°，

∴∠BOC=∠AOB+∠AOC=90°+60°=150°

故答案为：150°；

(2)∵OD平分∠BOC，OE平分∠AOC，

∴∠COD=∠BOC=75°,∠COE=∠AOC=30°，

∴∠DOE的度数为：∠COD∠COE=45°；

故答案为：45°；

(3)∵∠AOB=90°，∠AOC=2α，

∴∠BOC=90°+2α，

∵OD、OE平分∠BOC，∠AOC，

∴∠DOC=∠BOC=45°+α,∠COE=∠AOC=α，

∴∠DOE=∠DOC∠COE=45°.