
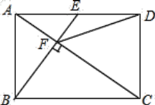
【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 边的中点,
边的中点,![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,有下列五个结论:①
,有下列五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A.1B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
①四边形ABCD是矩形,BE⊥AC,则∠ABC=∠AFB=90°,又∠BAF=∠CAB,于是△AEF∽△CAB;
②由![]() ,又AD∥BC,所以
,又AD∥BC,所以![]() ,故可得CF=2AE;
,故可得CF=2AE;
③过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出![]() ,得到CN=NF,根据线段的垂直平分线的性质可得结论;
,得到CN=NF,根据线段的垂直平分线的性质可得结论;
④设AE=a,AB=b,则AD=2a,由△BAE∽△ADC,得出![]() ,进而得出
,进而得出![]() ;
;
⑤由AE∥BC,推出![]() ,设S△AEF=S△DEF=m,推出S△ABF=2m,S△BFC=4m,S矩形ABCD=12m,S矩形BCDF=8m,推出S△ABF:S四边形BCDF=1:4,故⑤正确
,设S△AEF=S△DEF=m,推出S△ABF=2m,S△BFC=4m,S矩形ABCD=12m,S矩形BCDF=8m,推出S△ABF:S四边形BCDF=1:4,故⑤正确
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴![]() ,
,
∵AE=![]() AD=
AD=![]() BC,
BC,
∴![]() ,
,
∴CF=2AF,故②正确;
如图,过D作DM∥BE交AC于N,
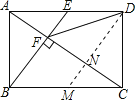
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=![]() BC,
BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DM垂直平分CF,
∴DF=DC,故③正确;
设AE=a,AB=b,则AD=2a,
由△BAE∽△ADC,有![]() ,即
,即![]() ,
,
所以,b=![]() ,
,
∴![]() ,故④错误;
,故④错误;
![]() ,
,
![]() ,
,
设![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
故⑤正确;
故选:D.


科目:初中数学 来源: 题型:
【题目】“校同安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
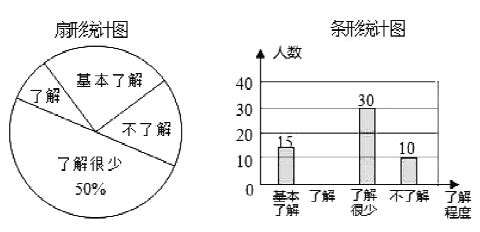
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 度;并补全条形统计图.
(2)若该中学共有学生![]() 人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为 人;
人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为 人;
(3)若从对校园安全知识达到“了解”程度的![]() 个女生
个女生![]() 和
和![]() 个男生
个男生![]() 中分别随机抽取
中分别随机抽取![]() 人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生
人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场部分平面图如图所示,C,E,A在同一直线上,D,E,B在同一直线上,测得A处与E处的距离为80 m,C处与D处的距离为34 m,∠C=90°,∠ABE=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
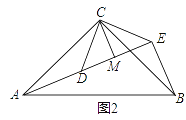
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
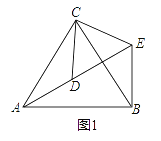
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
(3)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(Ⅰ)请求出∠AEB的度数;(Ⅱ)判断线段CM、AE、BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张阳把他和四位同学的年龄作为一组数据,计算出平均数是15,方差是0.4,则10年后张阳等5位同学的年龄的平均数和方差分别是( )
A.25和10.4B.15和4C.25和0.4D.15和0.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 分别交
分别交![]() 轴正半轴于点
轴正半轴于点![]() ,交
,交![]() 轴负半轴于点
轴负半轴于点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,且
,且![]() .
.
(1)如图1,求![]() 的值;
的值;
(2)如图![]() ,
,![]() 是第一象限抛物线上的点,连
是第一象限抛物线上的点,连![]() ,过点
,过点![]() 作
作![]() 轴,交
轴,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标以及
的坐标以及![]() 的值;
的值;
(3)如图3,在(2)的条件下,连接![]() ,
,![]() 是第一象限抛物线上的点(点
是第一象限抛物线上的点(点![]() 与点
与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 轴上(点
轴上(点![]() 在点
在点![]() 的左侧),
的左侧),![]() ,点
,点![]() 在直线
在直线![]() 上,连接
上,连接![]() 、
、![]() .若
.若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
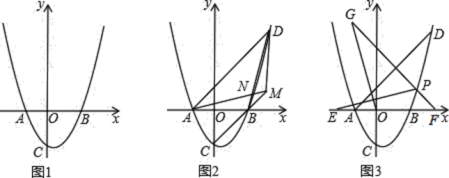
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点(与点A,B不重合),过点C作直线PQ,使得∠ACQ=∠ABC.
(1)求证:直线PQ是⊙O的切线.
(2)过点A作AD⊥PQ于点D,交⊙O于点E,若⊙O的半径为2,sin∠DAC=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个二次函数的图象经过点A(0,1),它的顶点为B(1,3).
(1)求这个二次函数的表达式;
(2)过点A作AC⊥AB交抛物线于点C,点P是直线AC上方抛物线上的一点,当△APC面积最大时,求点P的坐标和△APC的面积最大值.
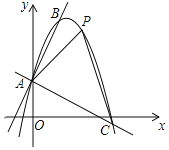
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王计划批发“山东大樱桃”和“泰国榴莲”两个品种的水果共120斤,樱桃和榴莲的批发价分别为32元/斤和40元/斤.设购买了樱桃x斤![]() .
.
(1)若小王批发这两种水果正好花费了4400元,那么小王分别购买了多少斤樱桃和榴莲?填写下表,并列方程求解;
品种 | 批发价(元) | 购买斤数 | 小王应付的钱数(元) |
樱桃 | 32 | x | |
榴莲 | 40 |
(2)设小王购买两种水果的总花费为y元,试写出y与x之间的函数表达式.
(3)若要求所批发的榴莲的斤数不少于樱桃斤数的2倍,那么购买樱桃的数量为多少时,可使小王的总花费最少?这个最少花费是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com