
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 在
在![]() 内并排
内并排![]() 不重叠
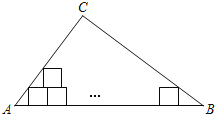
不重叠![]() 放入边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放
放入边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放![]()
![]() 个小正方形纸片.
个小正方形纸片.
A. 14个 B. 15个 C. 16个 D. 17个
【答案】C
【解析】分析:
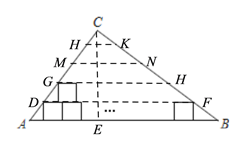
如下图,过点C作CE⊥AB于点E,则由已知条件易得CE=4.8,从而可知在△ABC内部,小正方形可以摆放4层,设这四层小正方形的上边沿所在直线分别与AC、BC相交于点D、F、G、H、M、N、K、H,则可得HK∥MN∥GH∥DF∥AB,由此结合已知条件求得DF、GH、MN、HK的长,即可知道每层可摆放的小正方形的个数,从而求得所求答案.
详解:
过点C作CE⊥AB于点E,
∵在Rt△ABC中,∠C=90°,AC=8,BC=6,
∴由勾股定理可得:AB=10,
∵S△ABC=![]() AB·CE=
AB·CE=![]() AC·BC,
AC·BC,
∴![]() ,解得CE=4.8,
,解得CE=4.8,
∴△ABC内部,小正方形可以摆放4层,
设这四层小正方形的上边沿所在直线分别与AC、BC相交于点D、F、G、H、M、N、K、H,则可得HK∥MN∥GH∥DF∥AB,
∵DF∥AB,小正方形的边长为1,
∴DF:AB=(4.8-1):4.8,解得DF=![]() ,
,
∴第一层可摆放小正方形7个,
同理可得第二层可摆放小正方形5个,第三层可摆放小正方形3个,第四层可摆放小正方形1个,
∴△ABC内部共可摆放小正方形16个.
故选C.


科目:初中数学 来源: 题型:
【题目】如图,某建筑工程队利用一面墙(墙的长度不限),用40米长的篱笆围成一个长方形的仓库.
(1)求长方形的面积是150平方米,求出长方形两邻边的长;
(2)能否围成面积220平方米的长方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一挖宝游戏,有一宝藏被随意藏在下面圆形区域内,(圆形区域被分成八等份)如图![]() .
.
(1)假如你去寻找宝藏,你会选择哪个区域(区域![]() ;区域
;区域![]() ;区域
;区域![]() )?为什么?在此区域一定能够找到宝藏吗?
)?为什么?在此区域一定能够找到宝藏吗?
(2)宝藏藏在哪两个区域的可能性相同?
(3)如果埋宝藏的区域如图![]() (图中每个方块完全相同),(1)(2)的结果又会怎样?
(图中每个方块完全相同),(1)(2)的结果又会怎样?

查看答案和解析>>
科目:初中数学 来源: 题型:
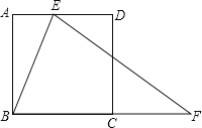
【题目】如图,E是正方形ABCD的边AD上的动点,F是边BC延长线上的一点,且BF=EF,AB=12,设AE=x,BF=y.
(1)当△BEF是等边三角形时,求BF的长;
(2)求y与x的函数解析式,并写出它的定义域;
(3)把△ABE沿着直线BE翻折,点A落在点A′处,试探索:△A′BF能否为等腰三角形?如果能,请求出AE的长;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC中,把AB绕点A按顺时针方向旋转α(0°<α<180°)得到AB′,把AC绕点A按逆时针方向旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB′C′是△ABC的“旋补三角形”,△AB′C′边B′C′上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
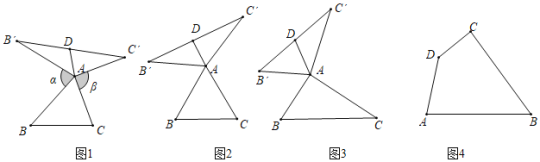
(1)特例感知:在图2、图3中,△AB′C′是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD=______BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为______.
(2)精确作图:如图4,已知在四边形ABCD内部存在点P,使得△PDC是△PAB的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点P(要求:保留作图痕迹,不写作法和证明)
(3)猜想论证:在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
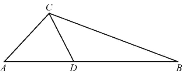
【题目】经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
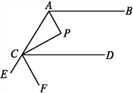
【题目】如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
(1)用α表示∠ACP;
(2)求证:AB∥CD;
(3)若AP∥CF,求证:FC平分∠DCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
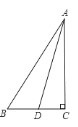
【题目】△ABC中,∠C=90°,∠BAC的平分线交BC于D,且CD=15,AC=30,则AB的长为( )
A. 30 B. 40 C. 50 D. 60
查看答案和解析>>
科目:初中数学 来源: 题型:
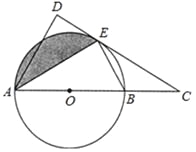
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的长;
②求出图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com