
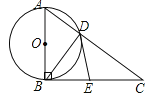
【题目】如图,已知Rt△ABC,∠ABC=90°,以直角边AB为直径作⊙O,交斜边AC于点D,连接BD.
(1)若AD=3,BD=4,求边BC的长;
(2)取BC的中点E,连接ED,试证明:ED与⊙O相切.
【答案】(1)![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】
试题(1)根据勾股定理易求AC的长,根据△ABD∽△ACB得比例线段可求BD的长.
(2)连接OD,证明DE⊥OD.
试题解析:(1)∵AB为直径,
∴∠ADB=90°,即BD⊥AC.
在Rt△ABC中,∵AB=3,BC=4,
∴由勾股定理得AC=5.
∵∠ABC=90°,BD⊥AC,
∴△ABD∽△ACB,
∴![]() ,
,
即![]() ,
,
∴BD=![]() ;
;
(2)连接OD.
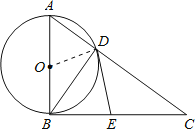
∵OD=OB(⊙O的半径),
∴∠OBD=∠BDO
∵AB是直径(已知),
∴∠ADB=90°(直径所对的圆周角是直角),
∴∠ADB=∠BDC=90°;
在Rt△BDC中,E是BC的中点,
∴BE=CE=DE(直角三角形斜边上的中线等于斜边的一半),
∴∠DBE=∠BDE
又∵∠ABC=∠OBD+∠DBE=90°,
∴∠ODE=∠BDO+∠BDE=90°(等量代换);
∵点D在⊙O上,
∴ED与⊙O相切.


科目:初中数学 来源: 题型:
【题目】如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是 ( )
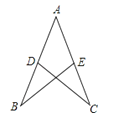
A. AB=AC B. ∠ADC=∠AEB C. ∠B=∠C D. BE=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
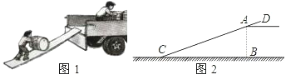
【题目】如图1是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图2中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,请求出木板CD的长度?
(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
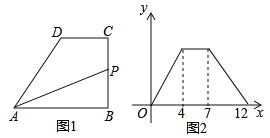
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 的方向运动,到达点
的方向运动,到达点![]() 停止,设点
停止,设点![]() 运动的路程为
运动的路程为![]() ,
,![]() 的面积为
的面积为![]() ,如果
,如果![]() 与
与![]() 的函数图象如图2所示,那么
的函数图象如图2所示,那么![]() 边的长度为______.
边的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB、AC上.

(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
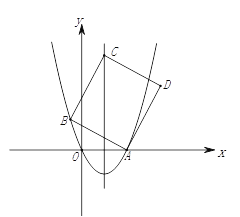
【题目】如图,抛物线![]() 交x轴的正半轴于点A,点B(
交x轴的正半轴于点A,点B(![]() ,a)在抛物线上,点C是抛物线对称轴上的一点,连接AB、BC,以AB、BC为邻边作□ABCD,记点C纵坐标为n,
,a)在抛物线上,点C是抛物线对称轴上的一点,连接AB、BC,以AB、BC为邻边作□ABCD,记点C纵坐标为n,
(1)求a的值及点A的坐标;
(2)当点D恰好落在抛物线上时,求n的值;
(3)记CD与抛物线的交点为E,连接AE,BE,当△AEB的面积为7时,n=___________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,动点E、F分别从点C,D出发,以相同速度分别沿CB,DC运动(点E到达C时,两点同时停止运动).连接AE,BF交于点P,过点P分别作PM∥CD,PN∥BC,则线段MN的长度的最小值为( )
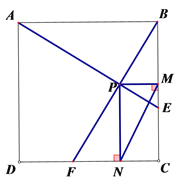
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三个形状大小相同的菱形按如图所示方式摆放,已知∠AOB=∠AOE=90°,菱形的较短对角线长为2cm.若点C落在AH的延长线上,则△ABE的周长为________cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com