
【题目】已知直线![]() ,
,
(1)如图1,点![]() 在直线
在直线![]() 上的左侧,直接写出
上的左侧,直接写出![]() ,
,![]() 和
和![]() 之间的数量关系是 .
之间的数量关系是 .
(2)如图2,点![]() 在直线
在直线![]() 的左侧,
的左侧,![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,直接写出
,直接写出![]() 和
和![]() 的数量关系是 .
的数量关系是 .
(3)如图3,点![]() 在直线
在直线![]() 的右侧
的右侧![]() ,
,![]() 仍平分
仍平分![]() ,
,![]() ,那么
,那么![]() 和
和![]() 有怎样的数量关系?请说明理由.
有怎样的数量关系?请说明理由.

【答案】(1) ![]() ;(2)
;(2)![]() ;
;
(3)![]() .理由见解析
.理由见解析
【解析】
(1)首先作EF∥AB,根据直线AB∥CD,可得EF∥CD,所以∠ABE=∠1,∠CDE=∠2,据此推得∠ABE+∠CDE=∠BED即可.
(2)首先根据BF,DF分别平分∠ABE,∠CDE,推得∠ABF+∠CFD=![]() (∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CFD,∠BED=∠ABE+∠CDE,据此推得∠BFD=
(∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CFD,∠BED=∠ABE+∠CDE,据此推得∠BFD=![]() ∠BED.
∠BED.
(3)首先过点E作EG∥CD,再根据AB∥CD,EG∥CD,推得AB∥CD∥EG,所以∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,据此推得∠ABE+∠CDE+∠BED=360°;然后根据∠BFD=∠ABF+∠CDF,以及BF,DF分别平分∠ABE,∠CDE,推得2∠BFD+∠BED=360°即可.
解:(1)如图1,作![]() ,
,
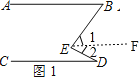 ,
,
![]() 直线
直线![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
即![]() .
.
(2)如图2,
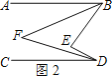 ,
,
![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
由(1),可得
![]()
![]() ,
,
![]() .
.
(3)如图3,过点![]() 作
作![]() ,
,
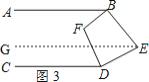 ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
由(1)知,![]() ,
,
又![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
故答案为:![]() 、
、![]() .
.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上以
上以![]() 的速度由
的速度由![]() 点向
点向![]() 点运动(点
点运动(点![]() 不与点
不与点![]() 重合),同时点
重合),同时点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点运动.
点运动.

(1)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,当运动时间是
的运动速度相等,当运动时间是![]() 时,
时,![]() 与
与![]() 是否全等?请说明理由;
是否全等?请说明理由;
(2)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当
的运动速度不相等,当![]() 与
与![]() 全等时,点
全等时,点![]() 的运动时间是_______________;运动速度是_________________.
的运动时间是_______________;运动速度是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,![]() 和
和![]() 是等腰直接角三角形,
是等腰直接角三角形,![]() ,点
,点![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,
,![]() 交于点
交于点![]() ,点
,点![]() 恰好是
恰好是![]() 中点,连接
中点,连接![]() .
.
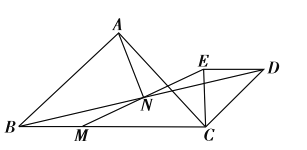
(1)求证:![]() ;
;
(2)连接AM、AE,请探究AN与EN的位置关系与数量关系。
①写出AN与EM:位置关系___;数量关系___;
②请证明上述结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,将三角形
为坐标原点,将三角形![]() 进行平移,平移后点
进行平移,平移后点![]() 的对应点分别是点
的对应点分别是点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若点![]() ,其中
,其中![]() . 直线
. 直线![]() 交
交![]() 轴于点
轴于点![]() ,且三角形
,且三角形![]() 的面积为1,试探究
的面积为1,试探究![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算a![]() b=a(1-b),下面给出了关于这种运算的四个结论:
b=a(1-b),下面给出了关于这种运算的四个结论:
①2![]() (-2)=6 ②a
(-2)=6 ②a![]() b=b
b=b![]() a
a
③若a+b=0,则(a![]() a)+(b
a)+(b![]() b)=2ab ④若a
b)=2ab ④若a![]() b=0,则a=0.
b=0,则a=0.
其中正确结论的序号是 (填上你认为所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
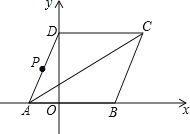
【题目】如图所示,菱形![]() 的顶点
的顶点![]() 在
在![]() 轴上,点
轴上,点![]() 在点
在点![]() 的左侧,点
的左侧,点![]() 在
在![]() 轴的正半轴上.点
轴的正半轴上.点![]() 的坐标为
的坐标为![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度,按照
出发,以每秒1个单位长度的速度,按照![]() 的顺序在菱形的边上匀速运动一周,设运动时间为
的顺序在菱形的边上匀速运动一周,设运动时间为![]() 秒.
秒.
(1)①点![]() 的坐标 .②求菱形
的坐标 .②求菱形![]() 的面积.
的面积.
(2)当![]() 时,问线段
时,问线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 最小,如果存在,求出
最小,如果存在,求出![]() 最小值;如果不存在,请说明理由.
最小值;如果不存在,请说明理由.
(3)若点![]() 到
到![]() 的距离是1,则点
的距离是1,则点![]() 运动的时间
运动的时间![]() 等于 .
等于 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是( )
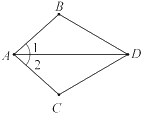
A. ∠ADB=∠ADCB. ∠B=∠CC. DB=DCD. AB=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车往返于甲、乙两地之间,如果汽车以50千米/时的平均速度从甲地出发,则6小时可到达乙地.
(1)写出时间t(时)关于速度v(千米/时)的函数关系式,并画出函数图象.
(2)若这辆汽车需在5小时内从甲地到乙地,则此时汽车的平均速度至少应是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com