
【题目】在平面直角坐标系中,![]() 为坐标原点,将三角形
为坐标原点,将三角形![]() 进行平移,平移后点
进行平移,平移后点![]() 的对应点分别是点
的对应点分别是点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若点![]() ,其中
,其中![]() . 直线
. 直线![]() 交
交![]() 轴于点
轴于点![]() ,且三角形
,且三角形![]() 的面积为1,试探究
的面积为1,试探究![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)![]() 的值为6;(2)
的值为6;(2)![]() .理由详见解析.
.理由详见解析.
【解析】
1)当a=1时,得出A、B、D、E四点的坐标,再根据平移的规律得到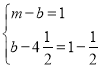 ,即可求出m的值;
,即可求出m的值;
(2)由平移的规律得出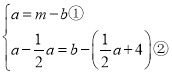 ,变形整理得到
,变形整理得到![]() ,那么CE∥x轴,根据三角形BEM的面积
,那么CE∥x轴,根据三角形BEM的面积![]() ,求出a=2,A(0,2),B(0,6),C(-2,5).根据点F与点C是对应点,得出F(0,4),求出AF=BF=2.
,求出a=2,A(0,2),B(0,6),C(-2,5).根据点F与点C是对应点,得出F(0,4),求出AF=BF=2.
解:(1)当![]() 时,
时,
由三角形![]() 平移得到三角形
平移得到三角形![]() ,
,
![]() 的对应点分别为
的对应点分别为
![]() ,
,![]()
可得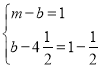 ,
,
解得![]() .
.
∴![]() 的值为6.
的值为6.
(2)由三角形![]() 平移得到三角形
平移得到三角形![]() ,
,
![]() ,
,![]() 的对应点分别为
的对应点分别为
![]() ,
,![]() .
.
可得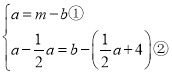 ,
,
由②得![]() ③,
③,
把③代入①,得![]() ,
,
∴![]() ,
,
∴点![]() 与点
与点![]() 的纵坐标相等,
的纵坐标相等,
∴![]() 轴,
轴,
∴点![]() ,
,
∴三角形![]() 的面积
的面积![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
又∵在平移中,点![]() 与点
与点![]() 是对应点,
是对应点,
∴![]() ,
,
∴![]()
![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
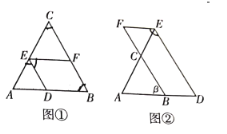
【题目】探究:如图①,在![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() ,
,![]() 上,且
上,且![]() ,
,![]() ∥
∥![]() ,若
,若![]() ,求
,求![]() 的度数.请把下面的解答过程补充完整.(请在空上填写推理依据或数学式子)
的度数.请把下面的解答过程补充完整.(请在空上填写推理依据或数学式子)
解:∵![]()
∴![]() ∥
∥![]() (_____________________________)
(_____________________________)
∴![]() ____________(_______________________)
____________(_______________________)
∵![]() ∥
∥![]()
∴_________![]() (_____________________)
(_____________________)
∴![]()
∵![]()
∴![]() _____________
_____________
应用:如图②,在![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() ,
,![]() 的延长线上,且
的延长线上,且![]() ,
,![]() ∥
∥![]() ,若
,若![]() ,则
,则![]() 的大小为_____________(用含
的大小为_____________(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() .点P第1次向右平移1个单位长度,向下平移2个单位长度至点
.点P第1次向右平移1个单位长度,向下平移2个单位长度至点![]() ,接着,第2次向右平移1个单位长度,向上平移3个单位长度至点
,接着,第2次向右平移1个单位长度,向上平移3个单位长度至点![]() ,第3次向右平移1个单位长度,向下平移4个单位长度至点
,第3次向右平移1个单位长度,向下平移4个单位长度至点![]() ,第4次向右平移1个单位长度,向上平移5个单位至点
,第4次向右平移1个单位长度,向上平移5个单位至点![]() ,…,按照此规律,点
,…,按照此规律,点![]() 第2019次平移至点
第2019次平移至点![]() 的坐标是
的坐标是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
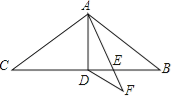
【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() ,
,
(1)如图1,点![]() 在直线
在直线![]() 上的左侧,直接写出
上的左侧,直接写出![]() ,
,![]() 和
和![]() 之间的数量关系是 .
之间的数量关系是 .
(2)如图2,点![]() 在直线
在直线![]() 的左侧,
的左侧,![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,直接写出
,直接写出![]() 和
和![]() 的数量关系是 .
的数量关系是 .
(3)如图3,点![]() 在直线
在直线![]() 的右侧
的右侧![]() ,
,![]() 仍平分
仍平分![]() ,
,![]() ,那么
,那么![]() 和
和![]() 有怎样的数量关系?请说明理由.
有怎样的数量关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
探究:要研究上面的问题,我们不妨先从最简单的情形入手,进而找到一般性规律.
探究一:将边长为2的正三角形的三条边分别二等分,连接各边中点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图①,连接边长为2的正三角形三条边的中点,从上往下看:
边长为1的正三角形,第一层有1个,第二层有3个,共有![]() 个;
个;
边长为2的正三角形一共有1个.

探究二:将边长为3的正三角形的三条边分别三等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图②,连接边长为3的正三角形三条边的对应三等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,共有![]() 个;边长为2的正三角形共有
个;边长为2的正三角形共有![]() 个.
个.

探究三:将边长为4的正三角形的三条边分别四等分(图③),连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)

结论:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)
应用:将一个边长为25的正三角形的三条边分别25等分,连接各边对应的等分点,则该三角形中边长为1的正三角形有______个和边长为2的正三角形有______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
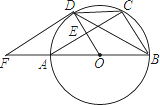
【题目】如图,AB是⊙O的直径,AC是弦,半径OD⊥AC于点E,过点D的切线与BA延长线交于点F.
(1)求证:∠CDB=∠BFD;
(2)若AB=10,AC=8,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com