【题目】在平面直角坐标系
中，点
.点P第1次向右平移1个单位长度，向下平移2个单位长度至点
，接着，第2次向右平移1个单位长度，向上平移3个单位长度至点
，第3次向右平移1个单位长度，向下平移4个单位长度至点
，第4次向右平移1个单位长度，向上平移5个单位至点
，…，按照此规律，点
第2019次平移至点
的坐标是
A.
B.
C.
D.
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】下列说法中正确的是（ ）
A.有且只有一条直线与已知直线垂直；
B.从直线外一点到这条直线的垂线段，叫做这点到这条直线距离；
C.互相垂直的两条线段一定相交；
D.直线
外一点
与直线上各点连接而成的所有线段中，最短线段的长度是
，则点到直线的距离是.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，对角线相交于点O，AC=AB， E是AB边的中点，G、F为 BC上的点，连接OG和EF，若AB=13， BC=10，GF=5，则图中阴影部分的面积为( )
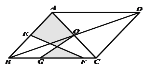
A.48B.36C.30D.24
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度，他们通过调整测量位置，使斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上，已知DE＝0.5米，EF＝0.25米，目测点D到地面的距离DG＝1.5米，到旗杆的水平距离DC＝20米，求旗杆的高度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如下图，
和
是等腰直接角三角形，
，点
为
边上一点，连接
，
交于点
，点恰好是中点，连接
.
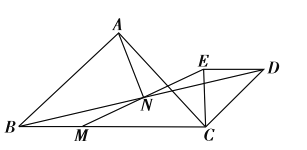
（1）求证：
；
（2）连接AM、AE，请探究AN与EN的位置关系与数量关系。
①写出AN与EM:位置关系___；数量关系___；
②请证明上述结论.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在第1个
中，
；在边
上任取一点
，延长
到
，使
，得到第2个
；在边
上任取一点
，延长
到
，使
，得到第3个
…按此做法继续下去，则第
个三角形中以
为顶点的底角度数是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，
为坐标原点，将三角形
进行平移，平移后点
的对应点分别是点
，点
，点
，点
，点
.
（1）若
，求
的值；
（2）若点
，其中
. 直线
交
轴于点
，且三角形
的面积为1，试探究
和
的数量关系，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
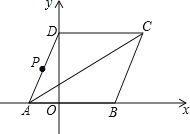
【题目】如图所示，菱形
的顶点
在
轴上，点
在点
的左侧，点
在
轴的正半轴上.点
的坐标为
.动点
从点出发，以每秒1个单位长度的速度，按照
的顺序在菱形的边上匀速运动一周，设运动时间为
秒.
(1)①点的坐标 .②求菱形的面积.
(2)当
时，问线段
上是否存在点
，使得
最小，如果存在，求出 最小值;如果不存在，请说明理由.
(3)若点到的距离是1，则点运动的时间等于 .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“格子乘法”是15世纪中叶，意大利数学家帕乔利在《算术几何及比例性质摘要》一书中介绍的一种两个数的相乘的计算方法．这种方法传入中国之后，在明朝数学家程大位的《算法统宗》书中被称为“铺地锦”具体步骤如下：
①先画一个矩形，把它分成p×q个方格（p，q分别为两乘数的位数）在方格上边、右边分别写下两个因数；
②再用对角线把方格一分为二，分别记录上述各位数字相应乘积的十位数与个位数；
③然后这些乘积由右下到左上，沿对角线方向相加，相加满十时向前进一；
④最后得到结果（方格左侧与下方数字依次排列）．比如：
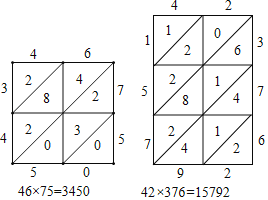
（1）图1是用“铺地锦”计算x9×784的格子，则z＝ ，x9×784＝
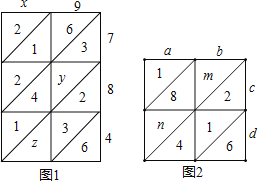
（2）图2是用“铺地锦”计算ab×cd的格子，已知ab×cd＝2176，求m和n的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
