
【题目】如图,在平行四边形ABCD中,对角线相交于点O,AC=AB, E是AB边的中点,G、F为 BC上的点,连接OG和EF,若AB=13, BC=10,GF=5,则图中阴影部分的面积为( )
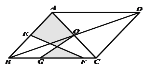
A.48B.36C.30D.24
科目:初中数学 来源: 题型:
【题目】如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2,以AD2为一边,做第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D3,以AD3为一边做第三个菱形AB3C3D3,使∠B3=60°,依此类推,这样做的第2020个菱形ABnCnDn的边ADn的长是( ).

A.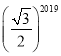 B.
B.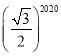 C.
C.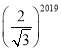 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
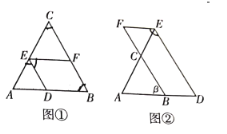
【题目】探究:如图①,在![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() ,
,![]() 上,且
上,且![]() ,
,![]() ∥
∥![]() ,若
,若![]() ,求
,求![]() 的度数.请把下面的解答过程补充完整.(请在空上填写推理依据或数学式子)
的度数.请把下面的解答过程补充完整.(请在空上填写推理依据或数学式子)
解:∵![]()
∴![]() ∥
∥![]() (_____________________________)
(_____________________________)
∴![]() ____________(_______________________)
____________(_______________________)
∵![]() ∥
∥![]()
∴_________![]() (_____________________)
(_____________________)
∴![]()
∵![]()
∴![]() _____________
_____________
应用:如图②,在![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() ,
,![]() 的延长线上,且
的延长线上,且![]() ,
,![]() ∥
∥![]() ,若
,若![]() ,则
,则![]() 的大小为_____________(用含
的大小为_____________(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆柱的底面半径是2cm,当圆柱的高h(cm)由大到小变化时,圆柱的体积V(cm3)随之发生变化。
(1)在这个变化过程中,自变量和因变量各是什么?
(2)在这个变化过程中,写出圆柱的体积为V与高h之间的关系式?
(3)当h由5cm变化到10cm时,V是怎样变化的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对篮球、足球、排球、羽毛球、乒乓球这五种球类运动的喜爱情况,随机抽取一部分学生进行问卷调查,统计整理并绘制了如图两幅不完整的统计图:
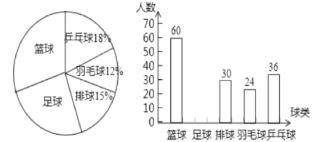
请根据以上统计图提供的信息,解答下列问题:
(1)共抽取___名学生进行问卷调查;
(2)补全条形统计图,求出扇形统计图中“篮球”所对应的圆心角的度数;
(3)该校共有2500名学生,请估计全校学生喜欢足球运动的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() .点P第1次向右平移1个单位长度,向下平移2个单位长度至点
.点P第1次向右平移1个单位长度,向下平移2个单位长度至点![]() ,接着,第2次向右平移1个单位长度,向上平移3个单位长度至点
,接着,第2次向右平移1个单位长度,向上平移3个单位长度至点![]() ,第3次向右平移1个单位长度,向下平移4个单位长度至点
,第3次向右平移1个单位长度,向下平移4个单位长度至点![]() ,第4次向右平移1个单位长度,向上平移5个单位至点
,第4次向右平移1个单位长度,向上平移5个单位至点![]() ,…,按照此规律,点
,…,按照此规律,点![]() 第2019次平移至点
第2019次平移至点![]() 的坐标是
的坐标是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
探究:要研究上面的问题,我们不妨先从最简单的情形入手,进而找到一般性规律.
探究一:将边长为2的正三角形的三条边分别二等分,连接各边中点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图①,连接边长为2的正三角形三条边的中点,从上往下看:
边长为1的正三角形,第一层有1个,第二层有3个,共有![]() 个;
个;
边长为2的正三角形一共有1个.

探究二:将边长为3的正三角形的三条边分别三等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图②,连接边长为3的正三角形三条边的对应三等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,共有![]() 个;边长为2的正三角形共有
个;边长为2的正三角形共有![]() 个.
个.

探究三:将边长为4的正三角形的三条边分别四等分(图③),连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)

结论:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)
应用:将一个边长为25的正三角形的三条边分别25等分,连接各边对应的等分点,则该三角形中边长为1的正三角形有______个和边长为2的正三角形有______个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com