
����Ŀ�����⣺���߳�Ϊ![]() ���������ε������߷ֱ�
���������ε������߷ֱ�![]() �ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬����������б߳�Ϊ1���������κͱ߳�Ϊ2���������ηֱ��ж��ٸ���
�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬����������б߳�Ϊ1���������κͱ߳�Ϊ2���������ηֱ��ж��ٸ���
̽����Ҫ�о���������⣬���Dz����ȴ�����������֣������ҵ�һ���Թ���.
̽��һ�����߳�Ϊ2���������ε������߷ֱ���ȷ֣����Ӹ����е㣬����������б߳�Ϊ1���������κͱ߳�Ϊ2���������ηֱ��ж��ٸ���
��ͼ�٣����ӱ߳�Ϊ2���������������ߵ��е㣬�������¿���
�߳�Ϊ1���������Σ���һ����1�����ڶ�����3��������![]() ����
����
�߳�Ϊ2����������һ����1��.

̽���������߳�Ϊ3���������ε������߷ֱ����ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬����������б߳�Ϊ1���������κͱ߳�Ϊ2���������ηֱ��ж��ٸ���
��ͼ�ڣ����ӱ߳�Ϊ3���������������ߵĶ�Ӧ���ȷֵ㣬�������¿����߳�Ϊ1���������Σ���һ����1�����ڶ�����3������������5��������![]() �����߳�Ϊ2���������ι���
�����߳�Ϊ2���������ι���![]() ��.
��.

̽���������߳�Ϊ4���������ε������߷ֱ��ĵȷ֣�ͼ�ۣ������Ӹ��߶�Ӧ�ĵȷֵ㣬����������б߳�Ϊ1���������κͱ߳�Ϊ2���������ηֱ��ж��ٸ���
����������������д��̽�����̣�

���ۣ����߳�Ϊ![]() ���������ε������߷ֱ�
���������ε������߷ֱ�![]() �ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬����������б߳�Ϊ1���������κͱ߳�Ϊ2���������ηֱ��ж��ٸ���
�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬����������б߳�Ϊ1���������κͱ߳�Ϊ2���������ηֱ��ж��ٸ���
����������������д��̽�����̣�
Ӧ�ã���һ���߳�Ϊ25���������ε������߷ֱ�25�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬����������б߳�Ϊ1������������______���ͱ߳�Ϊ2������������______��.
���𰸡�̽������16,6�����ۣ�n,![]() ;Ӧ�ã�625��300.
;Ӧ�ã�625��300.
��������
̽������ģ��̽��һ�������ɽ�����⣻
���ۣ���̽��һ���������ɵã����߳�Ϊ![]() ���������ε������߷ֱ�
���������ε������߷ֱ�![]() �ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬�߳�Ϊ1���������ι���
�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬�߳�Ϊ1���������ι���![]() �����߳�Ϊ2���������ι���
�����߳�Ϊ2���������ι���![]() ����
����
Ӧ�ã����ݽ��ۼ��ɽ������.
�⣺̽������
��ͼ3�����ӱ߳�Ϊ4���������������ߵĶ�Ӧ�ĵȷֵ㣬�������¿����߳�Ϊ1���������Σ���һ����1�����ڶ�����3������������5�������IJ���7��������![]() ����
����
�߳�Ϊ2������������![]() ��.
��.
���ۣ�
���ӱ߳�Ϊ![]() ���������������ߵĶ�Ӧ
���������������ߵĶ�Ӧ![]() �ȷֵ㣬�������¿����߳�Ϊ1���������Σ���һ����1�����ڶ�����3������������5�������IJ���7������������
�ȷֵ㣬�������¿����߳�Ϊ1���������Σ���һ����1�����ڶ�����3������������5�������IJ���7������������![]() ����
����![]() ��������
��������![]() ����
����
�߳�Ϊ2���������Σ�����![]() ��.
��.
Ӧ�ã�
�߳�Ϊ1������������![]() =625��������
=625��������
�߳�Ϊ2������������![]() ������.
������.
�ʴ�Ϊ��̽������16,6�����ۣ�n,![]() ;Ӧ�ã�625��300.
;Ӧ�ã�625��300.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У��Խ����ཻ�ڵ�O��AC=AB�� E��AB�ߵ��е㣬G��FΪ BC�ϵĵ㣬����OG��EF����AB=13�� BC=10��GF=5����ͼ����Ӱ���ֵ����Ϊ( )
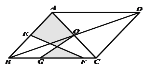
A.48B.36C.30D.24
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�![]() Ϊ����ԭ�㣬��������
Ϊ����ԭ�㣬��������![]() ����ƽ�ƣ�ƽ�ƺ��
����ƽ�ƣ�ƽ�ƺ��![]() �Ķ�Ӧ��ֱ��ǵ�
�Ķ�Ӧ��ֱ��ǵ�![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() .
.
��1����![]() ����
����![]() ��ֵ��
��ֵ��
��2������![]() ������
������![]() . ֱ��
. ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����������
����������![]() �����Ϊ1����̽��
�����Ϊ1����̽��![]() ��
��![]() ��������ϵ����˵������.
��������ϵ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
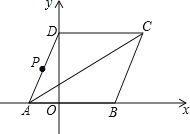
����Ŀ����ͼ��ʾ������![]() �Ķ���
�Ķ���![]() ��
��![]() ���ϣ���
���ϣ���![]() �ڵ�
�ڵ�![]() ����࣬��
����࣬��![]() ��
��![]() �����������.��
�����������.��![]() ������Ϊ
������Ϊ![]() .����
.����![]() �ӵ�
�ӵ�![]() ��������ÿ��1����λ���ȵ��ٶȣ�����
��������ÿ��1����λ���ȵ��ٶȣ�����![]() ��˳�������εı��������˶�һ�ܣ����˶�ʱ��Ϊ
��˳�������εı��������˶�һ�ܣ����˶�ʱ��Ϊ![]() ��.
��.
(1)����![]() ������ .��������
������ .��������![]() �����.
�����.
(2)��![]() ʱ�����߶�
ʱ�����߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ��С��������ڣ����
��С��������ڣ����![]() ��Сֵ;��������ڣ���˵������.
��Сֵ;��������ڣ���˵������.
(3)����![]() ��
��![]() �ľ�����1�����
�ľ�����1�����![]() �˶���ʱ��
�˶���ʱ��![]() ���� .
���� .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��˫����y��![]() ��һ�κ���y����x+4�ڵ�һ�����ڽ���A��B���㣬����AOB�����Ϊ2����k��ֵΪ�� ��
��һ�κ���y����x+4�ڵ�һ�����ڽ���A��B���㣬����AOB�����Ϊ2����k��ֵΪ�� ��

A.2B.![]() C.
C.![]() D.4
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
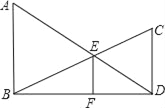
����Ŀ����֪����ͼ��AB��BD��CD��BD������ֱ�ΪB��D��AD��BC�ཻ�ڵ�E��EF��BD������ΪF�����ǿ���֤��![]() ��������Ҫ����֤������
��������Ҫ����֤������
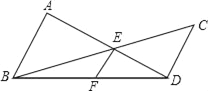
����ͼ�еĴ��߸�Ϊб������ͼ��AB��CD��AD��BC�ཻ�ڵ�E������E��EF��AB��BD�ڵ�F����
��1��![]() ����������������������֤�����������������˵�����ɣ�
����������������������֤�����������������˵�����ɣ�
��2�����ҳ�S��ABD��S��BED��S��BDC��Ĺ�ϵʽ��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1����2��Ҫ˵����ABD����ACD�����������������ѡһ���������ѡ���ǣ� ��
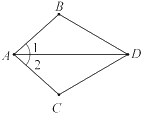
A. ��ADB����ADCB. ��B����CC. DB��DCD. AB��AC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ӳ˷�����15������Ҷ���������ѧ���������ڡ��������μ���������ժҪ��һ���н��ܵ�һ������������˵ļ��㷽�������ַ��������й�֮����������ѧ�ҳ̴�λ�ġ��㷨ͳ�ڡ����б���Ϊ���̵ؽ������岽�����£�
���Ȼ�һ�����Σ������ֳ�p��q������p��q�ֱ�Ϊ��������λ�����ڷ����ϱߡ��ұ߷ֱ�д������������
�����öԽ��߰ѷ���һ��Ϊ�����ֱ��¼������λ������Ӧ�˻���ʮλ�����λ����
��Ȼ����Щ�˻������µ����ϣ��ضԽ��߷�����ӣ������ʮʱ��ǰ��һ��
�����õ����������������·������������У������磺
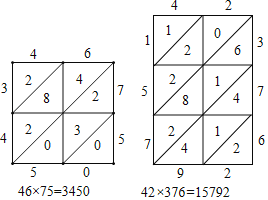
��1��ͼ1���á��̵ؽ�������x9��784�ĸ��ӣ���z���� ����x9��784���� ��
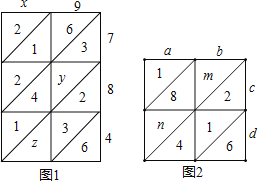
��2��ͼ2���á��̵ؽ�������ab��cd�ĸ��ӣ���֪ab��cd��2176����m��n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
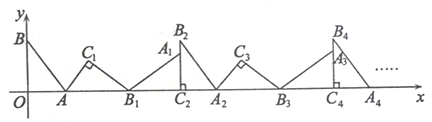
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABO�Ƶ�A˳ʱ����ת��![]() ��λ�ã���B��O�ֱ����ڵ�
��λ�ã���B��O�ֱ����ڵ�![]() ��
��![]() ������
������![]() ��x���ϣ��ٽ�
��x���ϣ��ٽ�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת��
˳ʱ����ת��![]() ��λ�ã���
��λ�ã���![]() ��x���ϣ���
��x���ϣ���![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת��
˳ʱ����ת��![]() ��λ�ã���
��λ�ã���![]() ��x���ϣ����ν�����ȥ������
��x���ϣ����ν�����ȥ������![]() ��
��![]() �����
�����![]() ������Ϊ________��
������Ϊ________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com