如图，将矩形纸片ABCD沿对角线BD折叠，使点A落在平面上的F点处，DF交BC于点E．
（1）求证：△DCE≌△BFE；
（2）若CD=2，∠ADB=30°，求BE的长．
快乐小博士巩固与提高系列答案科目：初中数学 来源： 题型：
将一次函数y=kx-1的图象向上平移k个单位后恰好经过点A（3，2+k）．
（1）求k的值；
（2）若一条直线与函数y=kx-1的图象平行，且与两个坐标轴所围成的三角形的面积为
，求该直线的函数关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
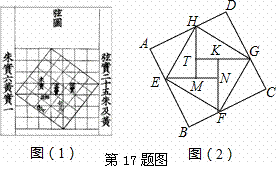
我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图（1））．图（2）由弦图变化得到，它是由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNK
T的面积分别为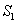
、
、
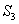．若正方形EFGH的边长为2，则
= ．
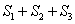查看答案和解析>>
科目：初中数学 来源： 题型：
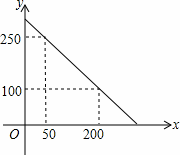
某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒，乙品牌的进货单价是甲品牌进货单价的2倍，考虑各种因素，预计购进乙品牌文具盒的数量y（个）与甲品牌文具盒的数量x（个）之间的函数关系如图所示．当购进的甲、乙品牌的文具盒中，甲有120个时，购进甲、乙品牌文具盒共需72
00元．
（1）根据图象
，求y与x之间的函数关系式；
（2）求甲、乙两种品牌的文具盒进货单价；
（3）若该超市每销售1个甲种品牌的文具盒可获利4元，每销售1个乙种品牌的文具盒可获利9元，根据学生需求，超市老板决定，准备用不超过6300元购进甲、乙两种品牌的文具盒，且这两种品牌的文具盒全部售出后获利不低于1795元，问该超市有几种进货方案？哪种
方案能使获利最大？最大获利为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，点C是线段AB的中点．
(1)若点D在线段CB上，且DB=3.5cm，AD=6.5cm，求线段CD的长度；
(2)若将(1)中的点“D在线段CB上”改为“点D在直线CB上”，其它条件不变，请画出相应的示意图，并求出此时线段CD的长度；
(3)若线段AB=12 cm，点C在AB上，点D、E分别是AC和BC的中点．
①当点C恰是AB中点时，则DE= cm．
②当AC=4 cm,时，求DE的长；
③当点C在线段AB上运动时(点C与A、B重合除外)，求DE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；
的相反数是 ，绝对值是 
的绝对值的相反数是_______．
-(1-0．5)×1/3×[4-(-2)3]