
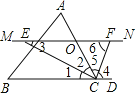
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.

(1)探究:线段OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
【答案】(1)OE=OF.(2)四边形BCFE不可能是菱形(3)当点O为AC中点且△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.
【解析】
试题分析:(1)利用平行线的性质由角相等得出边相等;
(2)假设四边形BCFE,再证明与在同一平面内过同一点有且只有一条直线与已知直线垂直相矛盾;
(3)利用平行四边形及等腰直角三角形的性质证明四边形AECF是正方形.
解:(1)OE=OF.
证明如下:
∵CE是∠ACB的平分线,
∴∠1=∠2.
∵MN∥BC,
∴∠1=∠3.
∴∠2=∠3.
∴OE=OC.
同理可证OC=OF.
∴OE=OF.(3分)
(2)四边形BCFE不可能是菱形,若四边形BCFE为菱形,则BF⊥EC,
而由(1)可知FC⊥EC,在平面内过同一点F不可能有两条直线同垂直于一条直线.(3分)
(3)当点O运动到AC中点时,且△ABC是直角三角形(∠ACB=90°)时,四边形AECF是正方形.
理由如下:
∵O为AC中点,
∴OA=OC,
∵由(1)知OE=OF,
∴四边形AECF为平行四边形;
∵∠1=∠2,∠4=∠5,∠1+∠2+∠4+∠5=180°,
∴∠2+∠5=90°,即∠ECF=90°,
∴AECF为矩形,
又∵AC⊥EF.
∴AECF是正方形.
∴当点O为AC中点且△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.(3分)


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
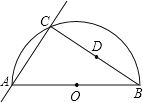
【题目】如图,AB是半圆O的直径,AB=10,过点A的直线交半圆于点C,且AC=6,连结BC,点D为BC的中点.已知点E在直线AC上,△CDE与△ACB相似,则线段AE的长为 3或 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于抛物线y=(x-1) +2,下列结论中不正确是 ( )
A. 对称轴为直线x=1 B. 当x<1时,y随x的增大而减小
C. 与x轴没有交点 D. 与y轴交于点(0,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铅笔每支售价0.20元,在平面直角坐标系内表示小明买1支到10支铅笔需要花费的钱数的图像是( )
A. 一条直线 B. 一条射线 C. 一条线段 D. 10个不同的点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】时代超市出售的三种品牌月饼袋上,分别标有质量为:(500±5)g、(500±10)g、(500±20)g的字样,从中任意拿出两袋,它们的质量最多相差( )
A.10g
B.20g
C.30g
D.40g
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度是( )
A. 第一次向右拐40, 第二次向左拐140
B. 第一次向左拐40, 第二次向右拐40
C. 第一次向左拐40, 第二次向左拐140
D. 第一次向右拐40, 第二次向右拐40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年1月1日新交通法规开始实施.为了解某社区居民遵守交通法规情况,小明随机选取部分居民就“行人闯红灯现象”进行问卷调查,调查分为“A:从不闯红灯;B:偶尔闯红灯;C:经常闯红灯;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2).请根据图中信息,解答下列问题:
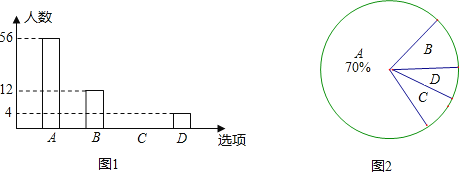
(1)本次调查共选取名居民;
(2)求出扇形统计图中“C”所对扇形的圆心角的度数,并将条形统计图补充完整;
(3)如果该社区共有居民1600人,估计有多少人从不闯红灯?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com