
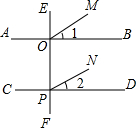
 如图,EF⊥AB,垂足为O,EF⊥CD,垂足为P,且∠1=∠2,说出OM与PN的位置关系,并说明理由.
如图,EF⊥AB,垂足为O,EF⊥CD,垂足为P,且∠1=∠2,说出OM与PN的位置关系,并说明理由. 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
| A、8.984×108 |
| B、8.98×108 |
| C、9×108 |
| D、9.0×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、0.5×1011 kg |
| B、50×109kg |
| C、5×1010kg |
| D、5.0×1010kg |
查看答案和解析>>
科目:初中数学 来源: 题型:
 前面的例题精讲中有这样一道题:如图①,在正方形ABCD中,点E在对角线BD上,求证:AE=CE.你看过了吗?如果看懂了请完成下题:如图②,在边长为2cm的正方形ABCD中,Q是边BC的中点,点P为对角线AC上一动点,连接PB,PQ.求△PBQ周长的最小值(结果不取近似值)
前面的例题精讲中有这样一道题:如图①,在正方形ABCD中,点E在对角线BD上,求证:AE=CE.你看过了吗?如果看懂了请完成下题:如图②,在边长为2cm的正方形ABCD中,Q是边BC的中点,点P为对角线AC上一动点,连接PB,PQ.求△PBQ周长的最小值(结果不取近似值)查看答案和解析>>
科目:初中数学 来源: 题型:
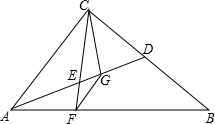 如图,△ABC中,∠ACB=90°,AD为BC边上的中线,点E为AD中点,CE的延长线交AB于点F,FG∥AC,交AD于点G,连接CG.求证:
如图,△ABC中,∠ACB=90°,AD为BC边上的中线,点E为AD中点,CE的延长线交AB于点F,FG∥AC,交AD于点G,连接CG.求证:查看答案和解析>>
科目:初中数学 来源: 题型:
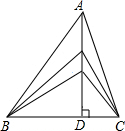 如图,△ABC边BC的长为10cm,BC边上的高为AD,当点A沿AD所在直线向点D运动时,三角形的面积发生了变化.
如图,△ABC边BC的长为10cm,BC边上的高为AD,当点A沿AD所在直线向点D运动时,三角形的面积发生了变化.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com