
 前面的例题精讲中有这样一道题:如图①,在正方形ABCD中,点E在对角线BD上,求证:AE=CE.你看过了吗?如果看懂了请完成下题:如图②,在边长为2cm的正方形ABCD中,Q是边BC的中点,点P为对角线AC上一动点,连接PB,PQ.求△PBQ周长的最小值(结果不取近似值)
前面的例题精讲中有这样一道题:如图①,在正方形ABCD中,点E在对角线BD上,求证:AE=CE.你看过了吗?如果看懂了请完成下题:如图②,在边长为2cm的正方形ABCD中,Q是边BC的中点,点P为对角线AC上一动点,连接PB,PQ.求△PBQ周长的最小值(结果不取近似值)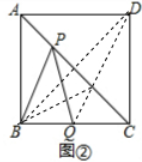 解:连接DQ,交AC于点P,连接BD.
解:连接DQ,交AC于点P,连接BD.| CD2+CQ2 |
| 22+12 |
| 5 |
| 5 |


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
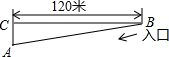 煤矿井下A点的海拔高度为-174.8米,已知从A到B的水平距离为120米,每经过水平距离10米,海拔上升(或下降)0.4米.
煤矿井下A点的海拔高度为-174.8米,已知从A到B的水平距离为120米,每经过水平距离10米,海拔上升(或下降)0.4米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com