
����Ŀ��ij�̳��ƻ��������䡢�ʵ�������ۣ������Ϣ���±���
���ۣ�Ԫ/̨�� | �ۼۣ�Ԫ/̨�� | |
���� |
| 2500 |
�ʵ� |
| 2000 |
��1�����̳���80000Ԫ�����������������64000Ԫ�����ʵ��������ȣ������a��ֵ��
��2��Ϊ�������г���Ҫ���̳������ò�����9��Ԫ�ɹ����䡢�ʵ繲50̨���ұ�������������ڲʵ�������![]() ��
��
�����̳����ļ��ֽ�����ʽ��
�������̳��������ı��䡢�ʵ�ȫ���۳�����õ��������ΪwԪ��������ѧ�ĺ���֪ʶ���w��ֵ��
���𰸡���1��2000��2���������ֽ�����ʽ��1������ʵ�25̨��������25̨��2������ʵ�26̨��������24̨��3������ʵ�27̨��������23̨����22500Ԫ��
��������
��1���ֱ��ʾ����Ͳʵ�Ĺ���������������ȹ�ϵ�з�����⣮
��2���蹺��ʵ�x̨�������䣨50��x��̨��
�����������в���ʽ����⣮
���ú�x�Ĵ���ʽ��ʾ����w������x��ȡֵ��Χ��һ�κ�����������⣮
��1�����������![]() �����a=2000��
�����a=2000��
������a=2000��ԭ���̵ĸ���
��a=2000��
��2���蹺��ʵ�x̨�������䣨50��x��̨��
�����������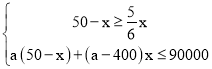 ����ã�
����ã�![]() ��
��
�������ֽ�����ʽ��
1������ʵ�25̨��������25̨��
2������ʵ�26̨��������24̨��
3������ʵ�27̨��������23̨��
��һ�����������Ϊ��500Ԫ��һ���ʵ������Ϊ400Ԫ��
��w=400x��500��50��x��=��100x+25000��
��wΪ����x��һ�κ�������Ϊ��������
��![]() ��xȡ������
��xȡ������
����x=25ʱ����õ�����������Ϊ22500Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2020��4��23�գ��ǵ�25����������գ�Ϊ�˽�ѧ��ÿ���Ķ�ʱ�䣬ijУ�����ȡ�˲���ѧ�����е��飬���ݵ����������Ķ�ʱ��x����λ��Сʱ���ֳ���4�飬A��0��x��2��B��2��x��4��C��4��x��6��D��6��x��8���Խ��ͼ��������Ϣ����������⣺
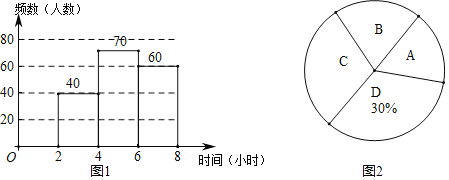
��1����������ȡ���� ����ѧ�����е��飻����ͳ��ͼ�У�����B��Բ�ĽǵĶ���Ϊ�� ����
��2����ȫƵ���ֲ�ֱ��ͼ��
��3������У����2000��ѧ�����Թ���ÿ���Ķ�ʱ�䲻����4Сʱ��ѧ�����ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧϰ��
�涨�������ɸ���ͬ������������������0���ij������������������2��2��2������3��������3��������3��������3���ȣ�����������ij˷������ǰ�2��2��2����2����������2��Ȧ3�η���������3��������3��������3��������3����������3��������������3��Ȧ4�η�����һ��أ��� ![]() ��a��0������a��������a��Ȧn�η�����
��a��0������a��������a��Ȧn�η�����
��1��������̽����
ֱ��д����������2��=_______����-![]() ����=_______��
����=_______��
��2��������˼����
����֪�����������ļ����������ת��Ϊ�ӷ����㣬�����������ת��Ϊ�˷����㣬�������ij����������ת��Ϊ�˷������أ�
��.��һ�ԣ������������ʽ��������������ֱ��д���ݵ���ʽ��
����3����=_______��5��=_______�� (-![]() ) ��=_______��
) ��=_______��
��. ��һ�룺��һ������������a��Ȧn�η�д���ݵ���ʽ����_______��
��. ��һ�㣺
12��(-![]() )����(-2)����(-
)����(-2)����(-![]() )����3.
)����3.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
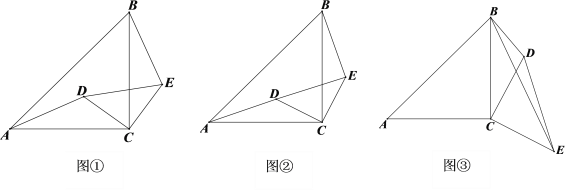
����Ŀ����ͼ����֪��ACB�͡�DCEΪ����ֱ�������Σ�����ͼ��λ�ðڷţ�ֱ�Ƕ���
C�غϣ�
��1����֤��AD=BE��
��2������DCE�Ƶ�C��ת�õ�ͼ�ڣ���A��D��E��ͬһֱ����ʱ����CD=![]() ,BE=3��
,BE=3��
��AB �ij���
��3������DCE�Ƶ�C˳ʱ����ת�õ�ͼ�ۣ�����CBD=45�㣬AC=6��BD=3����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ż�ʱ��С��һ������һ���С�γ�ȥ����̽��үү�����̺�������š����ϴӼ��������������6ǧ������������Ȼ����������1.5ǧ��үү�ң������үү�ҳ�����������12ǧ����ң����Ϸ��ؼ��
��1�����Լ�Ϊԭ�㣬��Ϊ��������1����λ���ȱ�ʾ1ǧ�ף��뽫���С�үү�Һ���ҵ�λ�������������Ϸֱ��õ�A��B��C��ʾ������
![]()
��2���ʳ���A�����C������ǧ�ף�
��3����С�γ�ÿǧ����0.08������С��һ�Ҵӳ��������ؼ�������·��С���ĺ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy��![]() ��ͼ
��ͼ![]() ����֪������
����֪������![]() ��������
��������![]() ��
��![]() ��
��

![]() ��������߶���C�����ꣻ
��������߶���C�����ꣻ
![]() ����AC��y���ڵ�D������BD��BC������C��
����AC��y���ڵ�D������BD��BC������C��![]() ������Ϊ��H�������߶Գ��ύx����G������HG����HG�ij���
������Ϊ��H�������߶Գ��ύx����G������HG����HG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
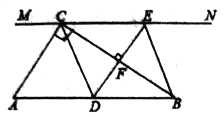
����Ŀ����ͼ����Rt��ABC�У���ACB=90��������C��ֱ��MN//AB��DΪAB��һ�㣬����D��DE��BC����ֱ��MN�ڵ�E������ΪF������CD��BE��
��1�����D��AB���е�ʱ���ı���BECD��ʲô�����ı��Σ�˵��������ɣ�
��2���ڣ�1���������£�����A= ʱ���ı���BECD�������Σ�˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�����֪��|a|�ļ�������������������a��Ӧ�ĵ���ԭ��ľ��룬��|a|��|a��0|��Ҳ����˵��|a|��ʾ����������a����0��Ӧ��֮��ľ��룮������ۿ����ƹ�Ϊ��|a��b|��ʾ����������a��b��Ӧ��֮��ľ��룮
��1����֪|a|��2����a��ֵ��
�⣺����������ԭ�����Ϊ2�ĵ�Ķ�Ӧ��Ϊ��2��2����a��ֵΪ2�ͩ�2��
��2����֪|a��1|��2����a��ֵ��
�⣺����������1�ľ���Ϊ2��Ķ�Ӧ��Ϊ3�ͩ�1����a��ֵΪ3�ͩ�1��
�����Ķ����ϵĽⷨ������������⣺
��1����֪|a|��![]() ����a��ֵ��
����a��ֵ��
��2����֪|a+2|��4����a��ֵ��
��3���������ϱ�ʾa�ĵ��ک�4��2֮�䣬��|a+4|+|a��2|��ֵΪ������
��4����a��������ʱ����|a+4|+|a��2|��ֵ��С����Сֵ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ͼ3�ǽ��������ȥһ���ֺ�õ��ļ����壮

(1)����Ҫ����д����
����/f | ������/v | ����/e | |
ͼ1 | _____ | _____ | ____ |
ͼ2 | _____ | _____ | _____ |
ͼ3 | ___ | _____ | ____ |
(2)����f��v��e����������Ĺ�ϵ��
(3)���ݲ�����㣬��һ��������Ķ�����2 019��������4 035�������������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com