
【题目】如图,已知二次函数y=ax2+bx+c的象经过A(﹣1,0)、B(3,0)、N(2,3)三点,且与y轴交于点C.
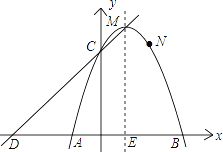
(1)求这个二次函数的解析式,并写出顶点M及点C的坐标;
(2)若直线y=kx+d经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;
(3)点P是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P,使以点P为圆心的圆经过A、B两点,并且与直线CD相切?如果存在,请求出点P的坐标;如果不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3,顶点M(1,4),点C(0,3);(2)见解析;
(3)点P存在,其坐标为(1,![]() )或(1,
)或(1,![]() ) .
) .
【解析】
(1)将点A、B、C的坐标代入y=ax2+bx+c中建立方程组,解方程组求得a、b、c的值即可得到所求的解析式,再由所得解析式求出顶点M的坐标和点C的坐标即可;
(2)根据(1)中所得点M、C的坐标求得直线CM的解析式,即可求得点D的坐标,然后结合已知条件证得CD=AN,AD=CN,即可证得四边形CDAN是平行四边形;
(3)如下图,若圆P过A、B两点,设点P的坐标为(1,y0),过点P作PQ⊥CM于点M,则当PQ=PA时,圆P和直线CM相切,由此结合已知条件列出关于y0的方程,解方程求出y0的值即可得到所求的点P的坐标.
(1)∵二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、B(3,0)、N(2,3)
∴可建立方程组: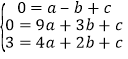 ,解得:
,解得: 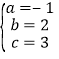 ,
,
∴所求二次函数的解析式为y=﹣x2+2x+3,
∵y=-(x-1)2+4,
∴顶点M的坐标为:(1,4),
∵在y=-x2+2x+3中,当x=0时,y=3,
∴点C的坐标为:(0,3)
(2)∵直线y=kx+d经过C、M两点,
∴ ![]() ,解得:即k=1,d=3,
,解得:即k=1,d=3,
∴直线CM的解析式为y=x+3.
∵在y=x+3中,当y=0时,x=﹣3,
∴点D的坐标为:(﹣3,0),
∵点C、A、N的坐标分别为(0,3)、(-1,0)、(2,3),
∴CD= ![]() ,AN=
,AN=![]() ,AD=2,CN=2,
,AD=2,CN=2,
∴CD=AN,AD=CN,
∴四边形CDAN是平行四边形;
(3)假设存在这样的点P,使以点P为圆心的圆经过A、B两点,并且与直线CD相切,
∵二次函数y=-(x-1)2+4的对称轴是直线x=1,
∴可设P的坐标为:(1,y0),
∴PA是圆P的半径且PA2=y02+22 ,
如下图,过点P做PQ⊥CD于Q,则当PQ=PA时,以P为圆心的圆与直线CD相切.
∵D、M、E的坐标分别为(-3,0)、(1,4)、(1,0),
∴DE=ME=4,ME⊥DE,
∴△MDE为等腰直角三角形,
∴△PQM也是等腰直角三角形,
由点P的坐标为(1,y0)可得PE=y0 ,
∴PM=|4﹣y0|,
∴![]() ,
,
由PQ2=PA2时,圆P和直线CM相切,可得方程:
![]() ,
,
解得![]() ,
,
∴满足题意的点P存在,其坐标为(1,![]() )或(1,
)或(1,![]() ) .
) .



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知甲、乙两袋中各装有若干颗球,其种类与数量如表所示.今阿冯打算从甲袋中抽出一颗球,小潘打算从乙袋中抽出一颗球,若甲袋中每颗球被抽出的机会相等,且乙袋中每颗球被抽出的机会相等,则下列叙述何者正确?( )
甲袋 | 乙袋 | |
红球 | 2颗 | 4颗 |
黄球 | 2颗 | 2颗 |
绿球 | 1颗 | 4颗 |
总计 | 5颗 | 10颗 |
A. 阿冯抽出红球的机率比小潘抽出红球的机率大
B. 阿冯抽出红球的机率比小潘抽出红球的机率小
C. 阿冯抽出黄球的机率比小潘抽出黄球的机率大
D. 阿冯抽出黄球的机率比小潘抽出黄球的机率小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
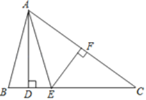
(1)若∠C=40°,求∠BAD的度数;
(2)若AC=5,DC=4,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由.
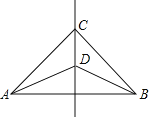
解:∵CD是线段AB的垂直平分线(已知),
∴AC=______,______=BD(______)
在△ADC和______中,
______=BC,
AD=______,
CD=______(______),
∴______≌______(______ ).
∴∠CAD=∠CBD (全等三角形的对应角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国学经典进校园,传统文化润心灵,某校开设了“围棋入门”、“诗歌汉字”、“翰墨飘香”、“史学经典”四门拓展课(每位学生必须且只选其中一门).
(1)学校对八年级部分学生进行选课调查,
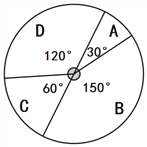

得到如图所示的统计图,请估计该校八年级420名学生选“诗歌汉字”的人数.
(2)“翰墨飘香”书画社的甲、乙、丙三人的书法水平相当,学校决定从这三名同学中任选两名参加市书法比赛,求甲和乙被选中的概率.(要求列表或画树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)因式分解:-28m3n2+42m2n3-14m2n
(2)因式分解:9a2(x-y)+4b2(y-x)
(3)求不等式![]() 的负整数解
的负整数解
(4)解不等式组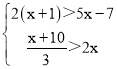 ,把它们的解集在数轴上表示出来.
,把它们的解集在数轴上表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级甲、乙两班分别选5名同学参加“奋发向上,崇德向善”演讲比赛,其预赛成绩如图所示:
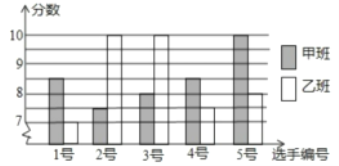
(1)根据上图填写下表:
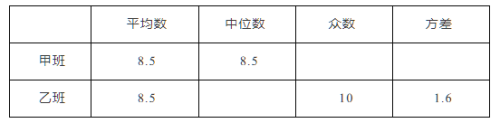
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪班的成绩较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
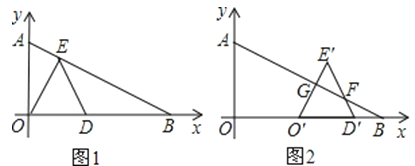
【题目】在Rt△ABO中,∠AOB=90°,OA=![]() ,OB=4,分别以OA、OB边所在的直线建立平面直角坐标系,D为x轴正半轴上一点,以OD为一边在第一象限内作等边△ODE.
,OB=4,分别以OA、OB边所在的直线建立平面直角坐标系,D为x轴正半轴上一点,以OD为一边在第一象限内作等边△ODE.
(1)如图①,当E点恰好落在线段AB上时,求E点坐标;
(2)在(Ⅰ)问的条件下,将△ODE沿x轴的正半轴向右平移得到△O′D′E′,O′E′、D′E′分别交AB于点G、F(如图②)求证OO′=E′F;
(3)若点D沿x轴正半轴向右移动,设点D到原点的距离为x,△ODE与△AOB重叠部分的面积为y,请直接写出y与x的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com