
【题目】在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,如果⊙O的半径为![]() ,
,
①请你判断M(2,0),N(﹣2,﹣1)两个点的变换点与⊙O的位置关系;
②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+6上,求点P与⊙O上任意一点距离的最小值.
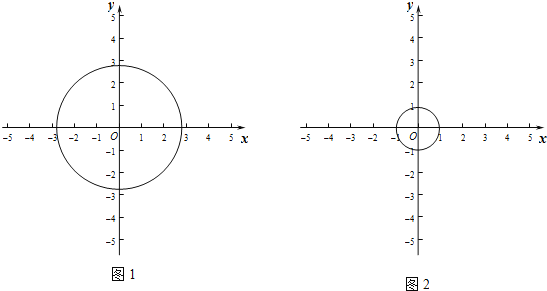
【答案】(1)①点N(﹣2,﹣1)的变换点在⊙O外;②点P横坐标的取值范围为﹣2<x<0;(2)点P与⊙O上任意一点距离的最小值为![]() ﹣1.
﹣1.
【解析】
试题分析:(1)①根据新定义得到点M的变换点M′的坐标为(2,2),于是根据勾股定理计算出OM′=2![]() ,则根据点与圆的位置关系的判定方法可判断点M的变换点在⊙O上;同样方法可判断点N(﹣2,﹣1)的变换点在⊙O外
,则根据点与圆的位置关系的判定方法可判断点M的变换点在⊙O上;同样方法可判断点N(﹣2,﹣1)的变换点在⊙O外
②利用一次函数图象上点的坐标特征,设P点坐标为(x,x+2),利用新定义得到P点的变换点为P′的坐标为(2x+2,﹣2),则根据勾股定理计算出OP′=![]() ,然后利用点与圆的位置关系得到
,然后利用点与圆的位置关系得到![]() <2
<2![]() ,解不等式得﹣2<x<0;
,解不等式得﹣2<x<0;
(2)设点P′的坐标为(x,﹣2x+6),P(m,n),根据新定义得到m+n=x,m﹣n=﹣2x+6,消去x得3m+n=6,则n=﹣3m+6,于是得到P点坐标为(m,﹣3m+6),则可判断点P在直线y=﹣3x+6上,设直线y=﹣3x+6与x轴相交于点A,与y轴相交于点B,过O点作OH⊥AB于H,交⊙O于C,如图2,易得A(2,0),B(0,6),利用勾股定理计算出AB=2![]() ,再利用面积法计算出OH=
,再利用面积法计算出OH=![]() ,所以CH=
,所以CH=![]() ﹣1,当点P在H点时,PC为点P与⊙O上任意一点距离的最小值.
﹣1,当点P在H点时,PC为点P与⊙O上任意一点距离的最小值.
解:(1)①M(2,0)的变换点M′的坐标为(2,2),则OM′=![]() =2
=2![]() ,所以点M(2,0)的变换点在⊙O上;
,所以点M(2,0)的变换点在⊙O上;
N(﹣2,﹣1)的变换点N′的坐标为(﹣3,﹣1),则ON′=![]() =
=![]() >2
>2![]() ,所以点N(﹣2,﹣1)的变换点在⊙O外;
,所以点N(﹣2,﹣1)的变换点在⊙O外;
②设P点坐标为(x,x+2),则P点的变换点为P′的坐标为(2x+2,﹣2),则OP′=![]() ,
,
∵点P′在⊙O的内,
∴![]() <2
<2![]() ,
,
∴(2x+2)2<4,即(x+1)2<1,
∴﹣1<x+1<1,解得﹣2<x<0,
即点P横坐标的取值范围为﹣2<x<0;
(2)设点P′的坐标为(x,﹣2x+6),P(m,n),
根据题意得m+n=x,m﹣n=﹣2x+6,
∴3m+n=6,
即n=﹣3m+6,
∴P点坐标为(m,﹣3m+6),
∴点P在直线y=﹣3x+6上,
设直线y=﹣3x+6与x轴相交于点A,与y轴相交于点B,过O点作OH⊥AB于H,交⊙O于C,如图2,
则A(2,0),B(0,6),
∴AB=![]() =2
=2![]() ,
,
∵![]() OHAB=
OHAB=![]() OAOB,
OAOB,
∴OH=![]() =
=![]() ,
,
∴CH=![]() ﹣1,
﹣1,
即点P与⊙O上任意一点距离的最小值为![]() ﹣1.
﹣1.



科目:初中数学 来源: 题型:
【题目】如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.
(1)请仅用无刻度的直尺,在⊙O中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法);
(2)请写出证明△ABC被所作弦分成的两部分面积相等的思路.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市天然气公司在一些居民小区安装天然气管道时,采用一种鼓励居民使用天然气的收费办法.若整个小区每户都安装,收整体初装费10000元,再对每户收费500元.某小区住户按这种收费方法全部安装天然气后,每户平均支付不足1000元,则这个小区的住户数( )
A. 至少20户 B. 至多20户
C. 至少21户 D. 至多21户
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)点A(3,-2)关于x轴的对称点的坐标是 .
(2).若点(a,-2)与点(-3,b)关于x轴对称,则a=__ __,b=__ __;若点(a,-2)与点(-3,b)关于y轴对称,则a=__ __,b=__ __.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com