
����Ŀ���������µ�������y��a��x+1����x��4����x��Ľ���ΪA��B��A��B����ߣ�����y�ύ�ڵ�C������AC��BC��
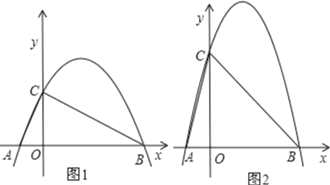
��1������ABC��ֱ�������Σ�ͼ1��������κ����Ľ���ʽ��
��2���ڣ�1���������£�����������y��ĸ���������ƽ��k��k��0������λ��ʹƽ�ƺ����������������ֻ���������㣬��k��ֵ��
��3������C����Ϊ��0��4��ʱ��ͼ2����P��Q����ͬʱ��C���������P������COB�˶�����B����Q�������ߣ��ڵ�һ���IJ��֣��˶�����B����P��Q������˶��ٶ���ͬ������˭�ȵ����B����˵�����ɣ����ο����ݣ�![]() .6��
.6��![]() ��
��
���𰸡���1��![]() ����2��
����2��![]() ����3����P�ȵ����B��
����3����P�ȵ����B��
��������
��1��������֪�������߽���ʽ�������A��B�����꣬��Rt��ABC�У�OC��AB��������Ӱ�����ĵõ�OC2=OAOB����������������֤�ã������ɵõ�OC�ij����Ӷ�ȷ��C������꣬������������ߵĽ���ʽ�У�����ȷ��a��ֵ���Ӷ�����������ߵĽ���ʽ��
��2�����ݣ�1�����������ߵĽ���ʽ��������䶥�����꣬���ں���ͼ���ƽ�Ʒ����Ѿ�ȷ��������y�Ḻ��������ƽ�ƣ�����������������ֻ���������㣬�������������
��C��O�غϣ���ʱ����������ƽ����OC������λ��
�������ߵĶ�������x���ϣ���ʱ����������ƽ�Ƶĵ�λ�����루1���������ߵĶ�����������ͬ��
�ۺ���������������������k��ֵ��
��3����C��0��4��ʱ���ɸ���������ȷ����ʱ�����ߵĽ���ʽ����������䶥��D�����ꣻP����ƶ���������ã���OC+OB������Q��Ĺ켣��һ�����ߣ���ֱ����ã������Ҫ����Ϊֱ����ӵĺ�P����ƶ�������бȽϣ�����CD��BD������B��C��D�������꣬�������CD��BD�ij����Ӷ�ȷ��BD+CDͬOC+OB�Ĵ�С��ϵ����ȻQ���ƶ�����Ҫ����CD+BD���������жϳ�P��Q�����·��˭��˭С������������ٶ���ͬ����ô·�̶̵ľ��ȵ���B�㣮
�⣺������y��a��x+1����x��4����x��Ľ���ΪA����1��0����B��4��0����
��1������ABC��ֱ�������Σ�ֻ�С�ACB��90����
�������á�ACO�ס�COB��
��![]() ��
��
��![]() ��
��
��CO��2
�������߿������£�
��C��0��2��
��C��0��2������ã�
��0+1����0��4��a��2��![]()
��![]() ��
��
��2����![]() �ɵã�
�ɵã�
�����ߵĶ���Ϊ��![]() ��
��![]() ������C��0��2����
������C��0��2����
����C����ƽ�Ƶ�ԭ��ʱ��
ƽ�ƺ����������������ֻ���������㣬
��k��2
����������ƽ�Ƶ�x��ʱ��
ƽ�ƺ����������������ֻ���������㣬
��![]() ��
��

��3������CΪ��0��4��ʱ�������ߵĽ���ʽΪy������x+1����x��4����
�����ߵĶ���ΪD��![]() ��
��![]() ��
��
����DC��DB
��D��![]() ��
��![]() ����B��4��0����C��0��4����
����B��4��0����C��0��4����
��CD��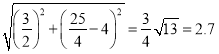 ��
��
DB�� ��
��
��CD+DB��2.7+6.75��9.45
��CO+OB��4+4��8��
��DB+DC��CO+OB
�ɺ���ͼ���֪��һ�����ڵ������ߵij��ȱ�CD+DB��Ҫ��
���Ե�һ�����ڵ������ߵij���Ҫ��������C��O��B�ij���
���Ե�P�ȵ����B��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
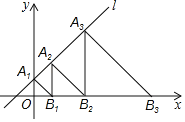
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��l��y��x+1��y���ڵ�A1����A2��A3������An��ֱ��l�ϣ���B1��B2��B3������Bn��x����������ϣ�����OA1B1����A2B1B2����A3B2B3��������AnBn��1Bn���ξ�Ϊ����ֱ�������Σ����B1��������_____����Bn��������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
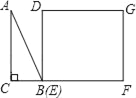
����Ŀ����ͼ����ABCΪֱ�������Σ���C=90�㣬BC=2cm����A=30�����ı���DEFGΪ���Σ�DE=2![]() cm��EF=6cm���ҵ�C��B��E��F��ͬһ��ֱ���ϣ���B���E�غϣ�Rt��ABC��ÿ��1cm���ٶ��ؾ���DEFG�ı�EF����ƽ�ƣ�����C���F�غ�ʱֹͣ����Rt��ABC�����DEFG���ص����ֵ����Ϊycm2���˶�ʱ��xs���ܷ�ӳycm2��xs֮�亯����ϵ�Ĵ���ͼ���ǣ�������
cm��EF=6cm���ҵ�C��B��E��F��ͬһ��ֱ���ϣ���B���E�غϣ�Rt��ABC��ÿ��1cm���ٶ��ؾ���DEFG�ı�EF����ƽ�ƣ�����C���F�غ�ʱֹͣ����Rt��ABC�����DEFG���ص����ֵ����Ϊycm2���˶�ʱ��xs���ܷ�ӳycm2��xs֮�亯����ϵ�Ĵ���ͼ���ǣ�������
A. 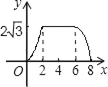 B.
B. 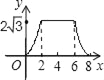 C.
C. 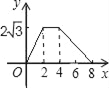 D.
D. 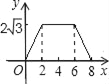
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
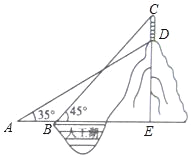
����Ŀ��ij�����˹���������һ����ɽ����ɽ������һ����Ľ�����CD����Ϊ10�ף���ѧС��Ϊ�˲�����ɽ�ĸ߶�DE���ڹ�����һˮƽ���棬��A����ý������D����ɽ����������Ϊ35�㣬��ˮƽ����ǰ��20����B�㣬��ý����ﶥ��C�������Ϊ45�㣬���ɽ�ĸ߶�DE���������ȷ��1�ף��ο����ݣ�sin35���![]() ��cos35���
��cos35���![]() ��tan35���
��tan35���![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������е�ÿ��С�����εı߳���Ϊ1��ÿ��С�����εĶ���и�㣮�������ͼ��ʾ�Ļ�ͼ��Ҫ�ٽ����̶ȵ�ֱ�ߣ��ڲ�д������������Ҫ�Ļ�ͼ�ۼ���
��1����ͼ1�л���һ����Ϊ![]() ���߶�MN��M��N�ֱ�Ϊ��㣩
���߶�MN��M��N�ֱ�Ϊ��㣩
��2����ͼ2�л���һ���Ը��Ϊ���㣬��ABΪһ�ߵ�������ABCD��
��3����ͼ3�У�E��F�ֱ�Ϊ��㣬�����߶�EF�Ĵ�ֱƽ����l��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪ���Σ���E�DZ�BC���е㣬AF��ED��AE��DF
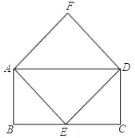
��1����֤���ı���AEDFΪ���Σ�
��2����̽������AB��BC���� ������AEDFΪ�����Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijƷ��ţ�̹�Ӧ���ṩA��B��C��D���ֲ�ͬ��ζ��ţ�̹�ѧ�����ã�ijУΪ���˽�ѧ���Բ�ͬ��ζ��ţ�̵�ϲ�ã���ȫУ��ţ�̵�ѧ��������������飬�����ݵ���������������������������ͳ��ͼ������ͳ��ͼ����Ϣ�������������

��1�����ε����ѧ���ж����ˣ�
��2����ȫ���������ͳ��ͼ��
��3������ͳ��ͼ��C��Ӧ�����ĽǶ�����_____��
��4������У��600��ѧ�����˸�Ʒ�Ƶ�ţ�̣�ÿ��ѧ��ÿ��ֻ��һ��ţ�̣�Ҫʹѧ���ܺȵ��Լ�ϲ����ţ�̣����ţ�̹�Ӧ��������У��ţ���У�A��B��ζ��ţ�̹�Լ���ٺУ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�MON�У��Ե�OΪԲ�ģ����ⳤΪ�뾶������������OM�ڵ�A��������ON�ڵ�B���ٷֱ���A��BΪԲ�ģ�OA�ij�Ϊ�뾶�����������ڡ�MON���ڲ����ڵ�C��������OC.��OA=5��AB=6�����B��AC�ľ���Ϊ�� ��
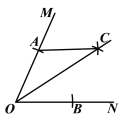
A. 5 B. ![]() C. 4 D.
C. 4 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
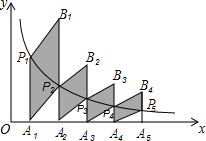
����Ŀ����ͼ���ֱ������������![]() ͼ���ϵĵ�P1(1��y1)��P2(2��y2)������Pn(n��Pn)������x��Ĵ��ߣ�����ֱ�ΪA1��A2������An ��������A1P2��A2P3������An��1Pn����������A1P1��A1P2Ϊһ���ڱ�һ��ƽ���ı���A1P1B1P2����A2P2��A2P3Ϊһ���ڱ�һ��ƽ���ı���A2P2B2P3���������ƣ����Bn����������______________��(����ú�n����ʽ��ʾ)
ͼ���ϵĵ�P1(1��y1)��P2(2��y2)������Pn(n��Pn)������x��Ĵ��ߣ�����ֱ�ΪA1��A2������An ��������A1P2��A2P3������An��1Pn����������A1P1��A1P2Ϊһ���ڱ�һ��ƽ���ı���A1P1B1P2����A2P2��A2P3Ϊһ���ڱ�һ��ƽ���ı���A2P2B2P3���������ƣ����Bn����������______________��(����ú�n����ʽ��ʾ)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com