【题目】如图，PA、PB分别切⊙O于点A、B，若∠P=70°，则∠C的大小为（度）．
【答案】55．
【解析】解：连接OA，OB，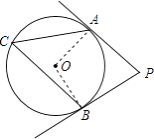 
∵PA、PB分别切⊙O于点A、B，
∴OA⊥PA，OB⊥PB，
即∠PAO=∠PBO=90°，
∴∠AOB=360°﹣∠PAO﹣∠P﹣∠PBO=360°﹣90°﹣70°﹣90°=110°，
∴∠C= 
∠AOB=55°．
所以答案是：55．
【考点精析】利用圆周角定理和切线的性质定理对题目进行判断即可得到答案，需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】“脐橙结硕果，香飘引客来”，赣南脐橙以其“外表光洁美观，肉质脆嫩，风味浓甜芳香”的特点饮誉中外.现欲将一批脐橙运往外地销售，若用2辆A型车和1辆B型车载满脐橙一次可运走10吨；用1辆A型车和2辆B型车载满脐橙一次可运走11吨.现有脐橙31吨，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满脐橙.
根据以上信息，解答下列问题：
（1）1辆A型车和1辆B型车都载满脐橙一次可分别运送多少吨？
（2）请你帮该物流公司设计租车方案；
（3）若1辆A型车需租金100元/次，1辆B型车需租金120元/次.请选出费用最少的租车方案，并求出最少租车费.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
（1）完成表中填空①；②；
（2）请计算甲六次测试成绩的方差；
（3）若乙六次测试成绩方差为 
，你认为推荐谁参加比赛更合适，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某车间有技术工人85人，平均每天每人可加工甲种部件16个或乙种部件10个，2个甲种部件和3个乙种部件配成一套，问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套？并求出加工了多少套？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，折叠边长为a的正方形ABCD，使点C落在边AB上的点M处（不与点A，B重合），点D落在点N处，折痕EF分别与边BC、AD交于点E、F，MN与边AD交于点G．证明：
（1）△AGM∽△BME；
（2）若M为AB中点，则 
；
（3）△AGM的周长为2a．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，长方体的长为15宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是（ ）
A. 20 B. 25 C. 30 D. 32
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过70千米
小时，如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路面对车速检测仪A的正前方60米处的C点，过了5秒后，测得小汽车所在的B点与车速检测仪A之间的距离为100米．
求BC间的距离；
这辆小汽车超速了吗？请说明理由．
【答案】这辆小汽车没有超速．
【解析】
（1）根据勾股定理求出BC的长；
（2）直接求出小汽车的时速，进行比较得出答案．
(1)在Rt△ABC中，AC＝60 m，
AB＝100 m，且AB为斜边，根据勾股定理，得BC＝80 m.
(2)这辆小汽车没有超速．
理由：∵80÷5＝16(m/s)，
而16 m/s＝57.6 km/h，57.6<70，
∴这辆小汽车没有超速．
【点睛】
考查勾股定理的应用，熟练掌握勾股定理是解题的关键.
【题型】解答题
【结束】
19
【题目】已知：如图，线段AC和BD相交于点G，连接AB，CD，E是CD上一点，F是DG上一点，
，且
．
求证：
；若
，
，求
的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
