
【题目】如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明:
(1)△AGM∽△BME;
(2)若M为AB中点,则 ![]() ;
;
(3)△AGM的周长为2a.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=90°,
∴∠AMG+∠AGM=90°,
∵EF为折痕,
∴∠GME=∠C=90°,
∴∠AMG+∠BME=90°,
∴∠AGM=∠BME,
在△AGM与△BME中,
∵∠A=∠B,∠AGM=∠BME,
∴△AGM∽△BME;
(2)解:∵M为AB中点,
∴BM=AM= ![]() ,
,
设BE=x,则ME=CE=a﹣x,
在Rt△BME中,∠B=90°,
∴BM2+BE2=ME2,即( ![]() )2+x2=(a﹣x)2,
)2+x2=(a﹣x)2,
∴x= ![]() a,
a,
∴BE= ![]() a,ME=
a,ME= ![]() a,
a,
由(1)知,△AGM∽△BME,
∴ ![]() =
= ![]() ,
,
∴AG= ![]() BM=
BM= ![]() a,GM=
a,GM= ![]() ME=
ME= ![]() a,
a,
∴ ![]() ;
;
(3)解:设BM=x,则AM=a﹣x,ME=CE=a﹣BE,
在Rt△BME中,∠B=90°,
∴BM2+BE2=ME2,即x2+BE2=(a﹣BE)2,
解得:BE= ![]() ,
,
由(1)知,△AGM∽△BME,
∴ ![]() ,
,
∵C△BME=BM+BE+ME=BM+BE+CE=BM+BC=a+x,
∴C△AGM=C△BME ![]() =(a+x)
=(a+x) ![]() =2a.
=2a.
【解析】(1)根据正方形和折叠的性质,得到两角对应相等,得到△AGM∽△BME;(2)由M为AB中点,再根据勾股定理和由(1)中的△AGM∽△BME,得到比例,证明出比例式;(3)根据勾股定理得到BE的代数式,再由(1)知,△AGM∽△BME,得到比例式,求出△AGM的周长为2a.
【考点精析】通过灵活运用翻折变换(折叠问题)和相似三角形的判定与性质,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.


科目:初中数学 来源: 题型:
【题目】某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品,5个福娃2枚徽章145元,10个福娃3枚徽章280元(5个福娃为1套),则:
(1)一套“福娃”玩具和一枚徽章的价格各是多少元?
(2)买5套“福娃”玩具和10枚徽章共需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )

A. 2![]() cm B. 3
cm B. 3![]() cm C. 4
cm C. 4![]() cm D. 3cm
cm D. 3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
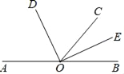
如图,已知点A,O,B在同一条直线上,OE平分∠BOC,∠DOE=90°
求证:OD是∠AOC的平分线;
证明:如图,因为OE是∠BOC的平分线,
所以∠BOE=∠COE.( )
因为∠DOE=90°
所以∠DOC+∠ =90°
且∠DOA+∠BOE=180°﹣∠DOE= °.
所以∠DOC+∠ =∠DOA+∠BOE.
所以∠ =∠ .
所以OD是∠AOC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:DC=BE;
(2)连接BF,若BF⊥AE,求证:△ADF≌△ECF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣x+m=0有两个不相等的实数根.
(1)求实数m的取值范围;
(2)若方程的两个实数根为x1、x2 , 且x1+x2+x1x2=m2﹣1,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移2格,再向上平移3格,其中每个格子的边长为1个单位长度。
(1)画出△ABC边AB上的高;
(2)请在图中画出平移后的三角形A’B’C’;
(3)若连接BB′,CC′,则这两条线段之间的关系是_____________________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com