
【题目】定义新运算:a※b=  ,则函数y=3※x的图象大致是( )
,则函数y=3※x的图象大致是( )
A.
B.
C.
D.
【答案】B
【解析】解:根据新定义运算可知,y=3※x= 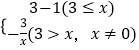 ,(1)当x≥3时,此函数解析式为y=2,函数图象在第一象限,以(3,2)为端点平行于x轴的射线,故可排除C、D;(2)当x<3时,此函数是反比例函数,图象在二、四象限,可排除A. 故选B.
,(1)当x≥3时,此函数解析式为y=2,函数图象在第一象限,以(3,2)为端点平行于x轴的射线,故可排除C、D;(2)当x<3时,此函数是反比例函数,图象在二、四象限,可排除A. 故选B.
【考点精析】利用一次函数的图象和性质和反比例函数的图象对题目进行判断即可得到答案,需要熟知一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,矩形OEFG的顶点E的坐标为(4,0),顶点G的坐标为(0,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM与GF交于点A.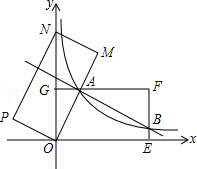
(1)求图象经过点A的反比例函数的解析式;
(2)设(2)中的反比例函数图象交EF于点B,直接写出直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是一段只有3米长的窄道路,由于一辆小汽车与一辆大卡车在AB段相遇,必须倒车才能继续通过.如果小汽车在AB段正常行驶需10分钟,大卡车在AB段正常行驶需20分钟,小汽车在AB段倒车的速度是它正常行驶速度的![]() ,大卡车在AB段倒车的速度是它正常行驶的
,大卡车在AB段倒车的速度是它正常行驶的![]() ,小汽车需倒车的路程是大卡车的4倍.问两车都通过AB这段狭窄路面的最短时间是 分钟.
,小汽车需倒车的路程是大卡车的4倍.问两车都通过AB这段狭窄路面的最短时间是 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F. 
(1)求证:BD是⊙O的切线.
(2)若AB= ![]() ,E是半圆
,E是半圆 ![]() 上一动点,连接AE,AD,DE. 填空:
上一动点,连接AE,AD,DE. 填空:
①当 ![]() 的长度是时,四边形ABDE是菱形;
的长度是时,四边形ABDE是菱形;
②当 ![]() 的长度是时,△ADE是直角三角形.
的长度是时,△ADE是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程kx2﹣(3k﹣1)x+2(k﹣1)=0
(1)求证:无论k为任何实数,方程总有实数根;
(2)若此方程有两个实数根x1 , x2 , 且|x1﹣x2|=2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1) (-4x2y)·(-x2y2)·(![]() y)3; (2) (-3ab)(2a2b+ab-1) ;
y)3; (2) (-3ab)(2a2b+ab-1) ;
(3) (m-![]() )(m+
)(m+![]() ); (4) (-x-1)(-x+1) ; (5) ( - x - 5)2 ; (6)
); (4) (-x-1)(-x+1) ; (5) ( - x - 5)2 ; (6)![]() ;
;
(7)先化简,再求值:(x+1)2﹣(x+2)(x﹣2),其中![]() ;
;
(8)解方程组![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上, ![]() 是
是![]() 的中点,
的中点, ![]() 是射线
是射线![]() 上一动点,且
上一动点,且![]() ,连接
,连接![]() ,作
,作![]() ,
, ![]() 交
交![]() 延长线于点
延长线于点![]() .
.
(![]() )如图
)如图![]() ,当点
,当点![]() 在
在![]() 上时,填空:
上时,填空: ![]() __________
__________ ![]() (填“
(填“![]() ”、“
”、“![]() ”或“
”或“![]() ”).
”).
(![]() )如图
)如图![]() ,当点
,当点![]() 在
在![]() 的延长线上时,请根据题意将图形补全,判断
的延长线上时,请根据题意将图形补全,判断![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com