
分析 (1)先计算零指数幂,平方,绝对值和负整数指数幂,再计算加减法;
(2)将除法变为乘法,再运用乘法的分配律计算;
(3)按照有理数混合运算的顺序,先乘方后乘除最后算加减,有括号的先算括号里面的.
解答 解:(1)20090-32+|-4|+($\frac{1}{2}$)-1
=1-9+4+2
=7-9
=-2;
(2)(-$\frac{3}{4}$-$\frac{5}{9}$+$\frac{7}{12}$)÷$\frac{1}{36}$
=(-$\frac{3}{4}$-$\frac{5}{9}$+$\frac{7}{12}$)×36
=-$\frac{3}{4}$×36-$\frac{5}{9}$×36+$\frac{7}{12}$×36
=-27-20+21
=-26;
(3)-12-[1$\frac{3}{7}$+(-12)÷6]2×(-$\frac{3}{4}$)3
=-1-[1$\frac{3}{7}$-2]2×(-$\frac{27}{64}$)
=-1-($\frac{4}{7}$)2×(-$\frac{27}{64}$)
=-1-$\frac{16}{49}$×(-$\frac{27}{64}$)
=-1+$\frac{27}{196}$
=-$\frac{169}{196}$.
点评 本题考查的是有理数的运算能力.注意:
(1)要正确掌握运算顺序,在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序;
(2)去括号法则:--得+,-+得-,++得+,+-得-.


科目:初中数学 来源: 题型:解答题
| 单价(元/件) | 25 | 28 | 35 | 40 | 42 |
| 销量(件) | 50 | 44 | 30 | 20 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+3x+2=x(x+3)+2 | B. | 4x2-9=(4x+3)(4x-3) | C. | x2-5x+6=(x-2)(x-3) | D. | a2-2a+1=(a+1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九2x=-6章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?”
《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九2x=-6章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?”| A. | 9x+11=6x-16 | B. | 9x-11=6x+16 | C. | $\frac{x-11}{9}=\frac{x+16}{6}$ | D. | $\frac{x+11}{9}=\frac{x-16}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
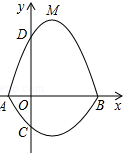 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com