
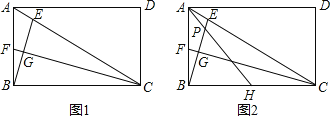
【题目】如图,在矩形ABCD中,点E是对角线AC上一动点,连接BE,作CF⊥BE分别交BE于点G,AB于点F.
(1)如图1,若CF恰好平分∠BCA,求证:△CGE≌△CGB;
(2)如图2,若![]() =
=![]() ,取BC的中点H,连接AH交BE于点P,求证:
,取BC的中点H,连接AH交BE于点P,求证:
①AH=3AP;
②BH2=BFBA.
【答案】(1)见解析;(2)①见解析;②见解析
【解析】
(1)根据ASA证明三角形全等即可.
(2)①延长BE交AD于T.利用平行线分线段成比例定理解决问题即可.
②证明△ABT∽△BCF,推出![]() 可得结论.
可得结论.
解:证明:(1)如图1中,
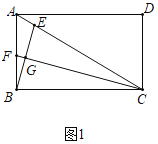
∵CF平分∠ACB,
∴∠ECG=∠BCG,
∵CF⊥BE,
∴∠CGB=∠CGE=90°,
∵CG=CG,
∴△CGE≌△CGB(ASA).
(2)①如图2中,延长BE交AD于T.
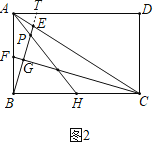
∵![]() ,
,
∴![]() ,
,
∵四边形ABCD是矩形,
∴AT∥BC,
∴![]() ,
,
∵BH=BC,
∴![]() ,
,
∴![]() ,
,
∴AH=3AP.
②∵四边形ABCD是矩形,
∴∠CBF=∠BAT=90°,
∵CF⊥BE,
∴∠ABT+∠TBC=90°,∠TBC+∠BCF=90°,
∴∠ABT=∠BCF,
∴△ABT∽△BCF,
∴![]() ,
,
∵AT=![]() BC=
BC=![]() BH,BC=2BH,
BH,BC=2BH,
∴BFBA=ATBC=![]() BH2BH=BH2,
BH2BH=BH2,
∴BH2=BFBA.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】某软件开发公司开发了A、B两种软件,每种软件成本均为1400元,售价分别为2000元、1800元,这两种软件每天的销售额共为112000元,总利润为28000元.
(1)该店每天销售这两种软件共多少个?
(2)根据市场行情,公司拟对A种软件降价销售,同时提高B种软件价格.此时发现,A种软件每降50元可多卖1件,B种软件每提高50元就少卖1件.如果这两种软件每天销售总件数不变,那么这两种软件一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了做好“营造清洁生活环境”活动的宣传,对本校学生进行了有关知识的测试,测试后随机抽取了部分学生的测试成绩,按“优秀、良好、及格、不及格”四个等级进行统计分析,并将分析结果绘制成如下两幅不完整的统计图:
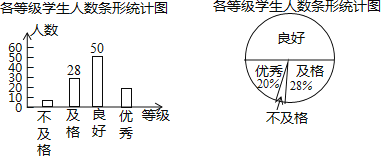
(1)求抽取的学生总人数;
(2)抽取的学生中,等级为“优秀”的人数为 人;扇形统计图中等级为“不合格”部分的圆心角的度数为 °;
(3)补全条形统计图;
(4)若该校有学生3500人,请根据以上统计结果估计成绩等级为“优秀”和“良好”的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
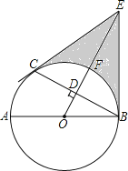
【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF = 2,BC = ![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
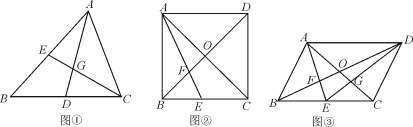
【题目】(1)证明推断:如图①,在△ABC中,D,E分别是边BC,AB的中点,AD,CE相交于点G,求证:![]() .
.
(2)类比探究:如图②,在正方形ABCD中,对角线AC、BD交于点O,E为边BC的中点,AE、BD交于点F,若AB=6,求OF的长;
(3)拓展运用:若正方形ABCD变为□ABCD,如图③,连结DE交AC于点G,若四边形OFEG的面积为![]() ,求□ABCD的面积.
,求□ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
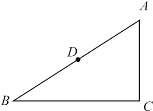
【题目】如图,在Rt△ABC中,∠C=90°,点D是AB的中点,AC<BC.
(1)试用无刻度的直尺和圆规,在BC上作一点E,使得直线ED平分ABC的周长;(不要求写作法,但要保留作图痕迹).
(2)在(1)的条件下,若DE分Rt△ABC面积为1﹕2两部分,请探究AC与BC的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com