
【题目】如图,在Rt△ABC中,∠C=90°,点D是AB的中点,AC<BC.
(1)试用无刻度的直尺和圆规,在BC上作一点E,使得直线ED平分ABC的周长;(不要求写作法,但要保留作图痕迹).
(2)在(1)的条件下,若DE分Rt△ABC面积为1﹕2两部分,请探究AC与BC的数量关系.
【答案】(1)作图见解析;(2)BC=3AC
【解析】
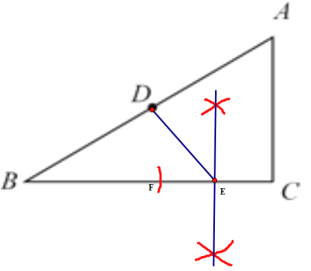
(1)在BC上用圆规截取BF=AC,然后再作FC的垂直平分线,其与BC的交点即为E点,最后连接DE即可.
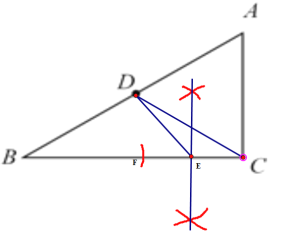
(2)连接DC,由点D是AB的中点,则S△ADC=S△BCD;设S△ADC=S△BCD=x,S△DEC=y,则有(x+y):(x-y)=2:1,解得x=3y,即E为BC的三等分点,即可说明BC=3EC;有EC=EF=BF=AC,即BC=3AC.
解:(1)如图:DE即为所求;
(2)连接DC
∵点D是AB的中点
∴S△ADC=S△BCD
设S△ADC=S△BCD=x,S△DEC=y,
∵S△BDC:S四边形CADE=1:2
∴(S△BDC -S△DCE):( S△ADC+S△DCE)=1:2,
∴2(x-y)=x+y,即x=3y
∴点E为BC的三等分点, 即BC=3EC
∵EC=EF=BF=AC
∴BC=3AC.


科目:初中数学 来源: 题型:
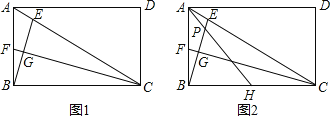
【题目】如图,在矩形ABCD中,点E是对角线AC上一动点,连接BE,作CF⊥BE分别交BE于点G,AB于点F.
(1)如图1,若CF恰好平分∠BCA,求证:△CGE≌△CGB;
(2)如图2,若![]() =
=![]() ,取BC的中点H,连接AH交BE于点P,求证:
,取BC的中点H,连接AH交BE于点P,求证:
①AH=3AP;
②BH2=BFBA.
查看答案和解析>>
科目:初中数学 来源: 题型:
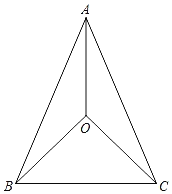
【题目】如图,在△ABC中,AB=AC,点O为∠BAC的平分线上一点,连接OB、OC.
(1)求证:OB=OC;
(2)若OA=OC,∠BAC=46°,求∠OCB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
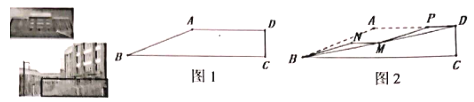
【题目】图1是我校闻澜阁前楼梯原设计稿的侧面图,![]() ,
,![]() ,楼梯
,楼梯![]() 的坡比为1:
的坡比为1:![]() ,为了增加楼梯的舒适度,将其改造成如图2,测量得
,为了增加楼梯的舒适度,将其改造成如图2,测量得![]() ,
,![]() 为
为![]() 的中点,过点
的中点,过点![]() 分别作
分别作![]() 交
交![]() 的角平分线于点
的角平分线于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,其中
,其中![]() 和
和![]() 为楼梯,
为楼梯,![]() 为平地,则平地
为平地,则平地![]() 的长度为_________
的长度为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=![]() ,若CE
,若CE![]() DE=5,则正方形的面积为( )
DE=5,则正方形的面积为( )
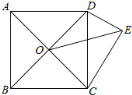
A.5B.6C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
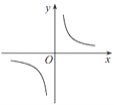
【题目】已知反比例函数 y=![]() 的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
A.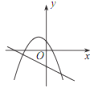 B.
B.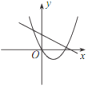 C.
C.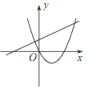 D.
D.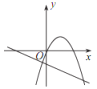
查看答案和解析>>
科目:初中数学 来源: 题型:
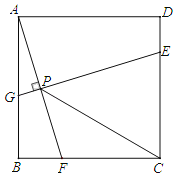
【题目】如图,已知四边形ABCD是边长为4的正方形,E为CD上一点,且DE=1,F为射线BC上一动点,过点E作EG⊥AF于点P,交直线AB于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45°时,BF=1;④PC的最小值为![]() ﹣2.其中正确的有( )
﹣2.其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F.
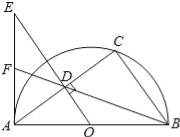
(1)求证:AEBC=ADAB;
(2)若半圆O的直径为10,sin∠BAC=![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com