
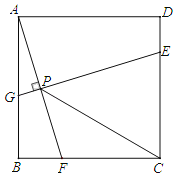
【题目】如图,已知四边形ABCD是边长为4的正方形,E为CD上一点,且DE=1,F为射线BC上一动点,过点E作EG⊥AF于点P,交直线AB于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45°时,BF=1;④PC的最小值为![]() ﹣2.其中正确的有( )
﹣2.其中正确的有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
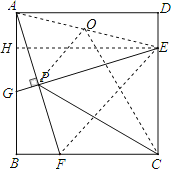
连接AE,过E作EH⊥AB于H,则EH=BC,根据全等三角形的判定和性质定理即可得到AF=EG,故①正确;根据平行线的性质和等腰三角形的性质即可得到PE=PC;故②正确;连接EF,推出点E,P,F,C四点共圆,根据圆周角定理得到∠FEC=∠FPC=45°,于是得到BF=DE=1,故③正确;取AE 的中点O,连接PO,CO,根据直角三角形的性质得到AO=PO=![]() AE,推出点P在以O为圆心,AE为直径的圆上,当O、C、P共线时,CP的值最小,根据三角形的三边关系得到PC≥OC﹣OP,根据勾股定理即可得到结论.
AE,推出点P在以O为圆心,AE为直径的圆上,当O、C、P共线时,CP的值最小,根据三角形的三边关系得到PC≥OC﹣OP,根据勾股定理即可得到结论.
连接AE,过E作EH⊥AB于H,
则EH=BC,
∵AB=BC,
∴EH=AB,
∵EG⊥AF,
∴∠BAF+∠AGP=∠BAF+∠AFB=90°,
∴∠EGH=∠AFB,
∵∠B=∠EHG=90°,
∴△HEG≌△ABF(AAS),
∴AF=EG,故①正确;
∵AB∥CD,
∴∠AGE=∠CEG,
∵∠BAF+∠AGP=90°,∠PCF+∠PCE=90°,
∵∠BAF=∠PCF,
∴∠AGE=∠PCE,
∴∠PEC=∠PCE,
∴PE=PC;故②正确;
连接EF,
∵∠EPF=∠FCE=90°,
∴点E,P,F,C四点共圆,
∴∠FEC=∠FPC=45°,
∴EC=FC,
∴BF=DE=1,
故③正确;
取AE 的中点O,连接PO,CO,
∴AO=PO=![]() AE,
AE,
∵∠APE=90°,
∴点P在以O为圆心,AE为直径的圆上,
∴当O、C、P共线时,CP的值最小,
∵PC≥OC﹣OP,
∴PC的最小值=OC﹣OP=OC﹣![]() AE,
AE,
∵OC=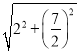 =
=![]() ,AE=
,AE=![]() =
=![]() ,
,
∴PC的最小值为![]() ﹣
﹣![]() ,故④错误,
,故④错误,
故选:C.
![]()


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
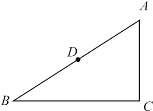
【题目】如图,在Rt△ABC中,∠C=90°,点D是AB的中点,AC<BC.
(1)试用无刻度的直尺和圆规,在BC上作一点E,使得直线ED平分ABC的周长;(不要求写作法,但要保留作图痕迹).
(2)在(1)的条件下,若DE分Rt△ABC面积为1﹕2两部分,请探究AC与BC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
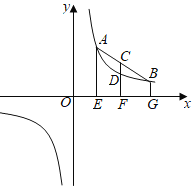
【题目】(1)阅读理解
如图,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上,连接
的图象上,连接![]() ,取线段
,取线段![]() 的中点
的中点![]() .分别过点
.分别过点![]() ,
,![]() ,
,![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,![]() ,
,![]() ,
,![]() 交反比例函数
交反比例函数![]() 的图象于点
的图象于点![]() .点
.点![]() ,
,![]() ,
,![]() 的横坐标分别为
的横坐标分别为![]() ,
,![]() ,
,![]() .小红通过观察反比例函数
.小红通过观察反比例函数![]() 的图象,并运用几何知识得出结论:AE+BG=2CF,CF>DF,由此得出一个关于
的图象,并运用几何知识得出结论:AE+BG=2CF,CF>DF,由此得出一个关于![]() ,
,![]() ,
,![]() 之间数量关系的命题:若
之间数量关系的命题:若![]() ,则______.
,则______.
(2)证明命题
小东认为:可以通过“若![]() ,则
,则![]() ”的思路证明上述命题.
”的思路证明上述命题.
小晴认为:可以通过“若![]() ,
,![]() ,且
,且![]() ,则
,则![]() ”的思路证明上述命题.
”的思路证明上述命题.
请你选择一种方法证明(1)中的命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
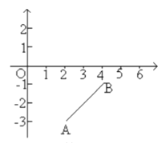
【题目】如图,已知平面直角坐标系,![]() 两点的坐标分别为
两点的坐标分别为![]() .
.
(1)若![]() 是
是![]() 轴上的一个动点,则当
轴上的一个动点,则当![]() _______时,
_______时,![]() 的周长最短;
的周长最短;
(2)若![]() 是
是![]() 轴上的两个动点,则当
轴上的两个动点,则当![]() _______时,四边形
_______时,四边形![]() 的周长最短;
的周长最短;
(3)设![]() 分别为
分别为![]() 轴和
轴和![]() 轴上的动点,请问:是否存在这样的点
轴上的动点,请问:是否存在这样的点![]() , 使四边形
, 使四边形![]() 的周长最短?若存在,请求出,
的周长最短?若存在,请求出,![]() _________,
_________,![]() ________(不必写解答过程);若不存在,请说明理由.
________(不必写解答过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
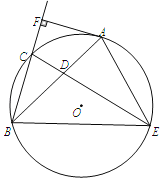
【题目】如图,已知AB是⊙O的弦,点C是弧AB的中点,D是弦AB上一动点,且不与A、B重合,CD的延长线交于⊙O点E,连接AE、BE,过点A作AF⊥BC,垂足为F,∠ABC=30°.
(1)求证:AF是⊙O的切线;
(2)若BC=6,CD=3,则DE的长为 ;
(3)当点D在弦AB上运动时,![]() 的值是否发生变化?如果变化,请写出其变化范围;如果不变,请求出其值.
的值是否发生变化?如果变化,请写出其变化范围;如果不变,请求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了提高学生的综合素质,成立了以下社团:![]() .机器人,
.机器人,![]() .围棋,
.围棋,![]() .羽毛球,
.羽毛球,![]() .电影配音.每人只能加入一个社团.为了解学生参加社团的情况,从加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下两幅不完整的统计图,其中图
.电影配音.每人只能加入一个社团.为了解学生参加社团的情况,从加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下两幅不完整的统计图,其中图![]() 中
中![]() 所占扇形的圆心角为
所占扇形的圆心角为![]() .
.
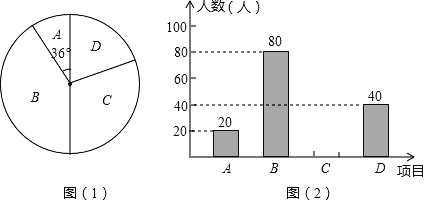
根据以上信息,解答下列问题:
![]() 这次被调查的学生共有 人;
这次被调查的学生共有 人;
![]() 请你将条形统计图补充完整;
请你将条形统计图补充完整;
![]() 若该校共有
若该校共有![]() 学生加入了社团,请你估计这
学生加入了社团,请你估计这![]() 名学生中有多少人参加了羽毛球社团;
名学生中有多少人参加了羽毛球社团;
![]() 在机器人社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加机器人大赛.用树状图或列表法求恰好选中甲、乙两位同学的概率.
在机器人社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加机器人大赛.用树状图或列表法求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系:
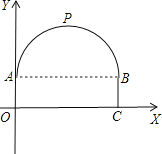
(1)求抛物线的解析式;
(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】忽如一夜春风来,千树万树梨花开.在清明假期期间,小梅和小北姐弟二人准备一起去乐陵大孙乡采摘园赏梨花,但因家中临时有事,必须留下一人在家,于是姐弟二人采用游戏的方式来确定谁去赏梨花.游戏规则是:在不透明的口袋中分别放入2个白色和1个黄色的乒乓球,它们除颜色外其余都相同.游戏时先由小梅从口袋中任意摸出1个乒乓球记下颜色后放回并摇匀,再由小北从口袋中摸出1个乒乓球,记下颜色.如果姐弟二人摸到的乒乓球颜色相同,则小梅赢,否则小北赢.则小北赢的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com