
【题目】如图,已知平面直角坐标系,![]() 两点的坐标分别为
两点的坐标分别为![]() .
.
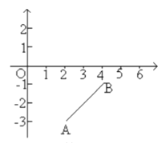
(1)若![]() 是
是![]() 轴上的一个动点,则当
轴上的一个动点,则当![]() _______时,
_______时,![]() 的周长最短;
的周长最短;
(2)若![]() 是
是![]() 轴上的两个动点,则当
轴上的两个动点,则当![]() _______时,四边形
_______时,四边形![]() 的周长最短;
的周长最短;
(3)设![]() 分别为
分别为![]() 轴和
轴和![]() 轴上的动点,请问:是否存在这样的点
轴上的动点,请问:是否存在这样的点![]() , 使四边形
, 使四边形![]() 的周长最短?若存在,请求出,
的周长最短?若存在,请求出,![]() _________,
_________,![]() ________(不必写解答过程);若不存在,请说明理由.
________(不必写解答过程);若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在使四边形
;(3)存在使四边形![]() 周长最短的点
周长最短的点![]() ,
,![]() .
.
【解析】
(1)根据题意,设出并找到点B(4,-1)关于x轴的对称点坐标为(4,1),进而可得直线AB'的解析式,然后得出答案;
(2)过A点作AE⊥x轴于点E且延长AE,取A'E= AE作点F(1,-1),连接A'F利用两点,间线段最短,可知四边形A BCD的周长最短等于A'F+CD + AB从而确定C点的坐标值;
(3)存在使四边形ABMN的周长最短的点M,N,作A关于y轴的对称点A',作B关于x轴的对称点是AF连接A'B'与x轴,y轴的交点即为点M,N,所以A'(-2,-3), B'(4,1),所以直线A'B'的解析式为:![]() ,从而得到m,n.
,从而得到m,n.
(1)设点B(4,-1)关于x轴的对称点坐标为(4,1),
设直线AB'的解析式为y= kx+ b,
把A(2, -3),B'(4,1)代入得:
![]() ,
,
解得:![]() ,
,
所以y=2x- 7,
令y= 0得![]() ,
,
即![]() ;
;
(2)过A点作AE⊥x轴于点E且延长AE,取A'E= AE,作点F(1,-1),
连接A'F,则A'(2,3),
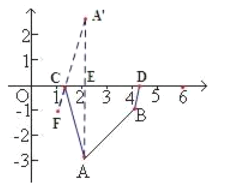
直线A'F的解析式为![]()
即y=4x- 5,
∵C(a,0),且点C在直线A'F上,
∴![]() ;
;
(3)存在使四边形ABMN的周长最短的点M,N;
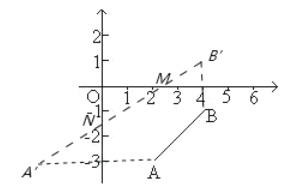
作A关于y轴的对称点A',作B关于x轴的对称点B',连接A'B'与x轴,y轴的交点即为点M,N,设直线A'B'的解析式为:![]() ;
;
∴A'(-2,-3), B'(4,1),
∴直线A'B'的解析式为:![]() ,
,
从而得到![]() ,
,
∴m=![]() ,n
,n![]() .
.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:
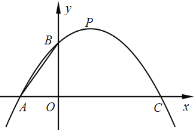
【题目】如图,二次函数![]() (a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(1)求 A、C 两点坐标;
(2)过点 B 作 BD∥x 轴交抛物线于 D,过点 P 作 PE∥AB 交 x 轴于 E,连接 DE,
①求 E 坐标;
②若 tan∠BPM=![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=![]() ,若CE
,若CE![]() DE=5,则正方形的面积为( )
DE=5,则正方形的面积为( )
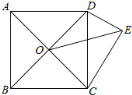
A.5B.6C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
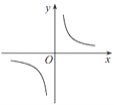
【题目】已知反比例函数 y=![]() 的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
A.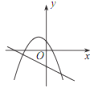 B.
B.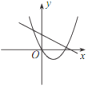 C.
C.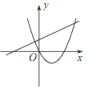 D.
D.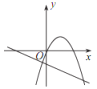
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电子跳蚤游戏盘是如图所示的![]() ,
,![]() .如果跳蚤开始时在
.如果跳蚤开始时在![]() 边的
边的![]() 处,
处,![]() .跳蚤第一步从
.跳蚤第一步从![]() 跳到
跳到![]() 边的
边的![]() (第1次落点)处,且
(第1次落点)处,且![]() ;第二步从
;第二步从![]() 跳到
跳到![]() 边的
边的![]() (第2次落点)处,且
(第2次落点)处,且![]() ;第三步从
;第三步从![]() 跳到
跳到![]() 边的
边的![]() (第3次落点)处,且
(第3次落点)处,且![]() ;……;跳蚤按上述规则一直跳下去,第
;……;跳蚤按上述规则一直跳下去,第![]() 次落点为
次落点为![]() (
(![]() 为正整数),则点
为正整数),则点![]() 与
与![]() 之间的距离为( )
之间的距离为( )
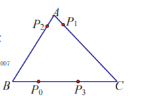
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是边长为4的正方形,E为CD上一点,且DE=1,F为射线BC上一动点,过点E作EG⊥AF于点P,交直线AB于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45°时,BF=1;④PC的最小值为![]() ﹣2.其中正确的有( )
﹣2.其中正确的有( )
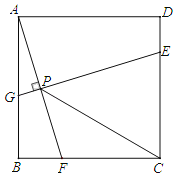
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是![]() ,类似地,图2所示的算筹图我们可以表述为( )
,类似地,图2所示的算筹图我们可以表述为( )
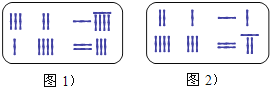
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:
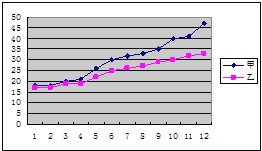
对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )
A.甲运动员得分的极差大于乙运动员得分的极差B.甲运动员得分的的中位数大于乙运动员得分的的中位数
C.甲运动员的得分平均数大于乙运动员的得分平均数D.甲运动员的成绩比乙运动员的成绩稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为改善办学条件,计划购进A,B两种规格的书架,经市场调查发现有线下和线上两种购买方式,具体情况如下表:

(1)如果在线下购买A,B两种书架20个,共花费5520元,求A,B两种书架各购买了多少个.
(2)如果在线上购买A,B两种书架20个,共花费W元,设其中A种书架购买m个,求W关于m的函数关系式.
(3)在(2)的条件下,若购买B种书架的数量不少于A种书架数量的2倍,请求出花费最少的购买方案,并计算按照这种购买方案,线上比线下节约多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com