
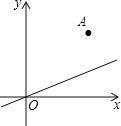
【题目】如图,已知点A(1,1)关于直线y =kx的对称点恰好落在x轴的正半轴上,则k的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
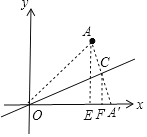
作辅助线,构建点与x轴和y轴的垂线,先根据点A的坐标得出OA′的长,再根据中位线定理和推论得:CF是△AA′E的中位线,所以CF=![]() AE=
AE=![]() ,也可以求OF的长,表示出点C的坐标,代入直线y=kx中求出k的值.
,也可以求OF的长,表示出点C的坐标,代入直线y=kx中求出k的值.
解:设A关于直线y=kx的对称点为A′,连接AA′,交直线y=kx于C,分别过A、C作x轴的垂线,垂足分别为E、F,则AE∥CF,
∵A(1,1),
∴AE=OE=1,
∴OA=![]() ,
,
∵A和A′关于直线y=kx对称,
∴OC是AA′的中垂线,
∴OA′=OA=![]() ,
,
∵AE∥CF,AC=A′C,
∴EF=A′F=![]() ,
,
∴CF=![]() AE=
AE=![]() ,
,
∴OF=OA′-A′F=![]() ,
,
∴C(![]() ,
,![]() ),
),
把C(![]() ,
,![]() )代入y=kx中得:
)代入y=kx中得:
![]() ,
,
∴![]() ,
,
故选:B.


科目:初中数学 来源: 题型:
【题目】青海新闻网讯:2016年2月21日,西宁市首条绿道免费公共自行车租赁系统正式启用.市政府今年投资了112万元,建成40个公共自行车站点、配置720辆公共自行车.今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2018年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)请你求出2016年到2018年市政府配置公共自行车数量的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
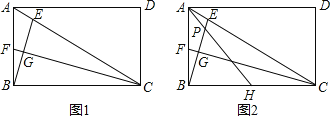
【题目】如图,在矩形ABCD中,点E是对角线AC上一动点,连接BE,作CF⊥BE分别交BE于点G,AB于点F.
(1)如图1,若CF恰好平分∠BCA,求证:△CGE≌△CGB;
(2)如图2,若![]() =
=![]() ,取BC的中点H,连接AH交BE于点P,求证:
,取BC的中点H,连接AH交BE于点P,求证:
①AH=3AP;
②BH2=BFBA.
查看答案和解析>>
科目:初中数学 来源: 题型:
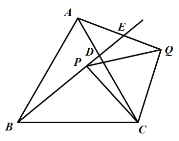
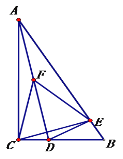
【题目】如图,在边长为 6 的等边△ABC 中,D 为 AC 上一点,AD=2,P 为 BD 上一点,连接 CP,以 CP 为 边,在 PC 的右侧作等边△CPQ,连接 AQ 交 BD 延长线于 E,当△CPQ 面积最小时,QE=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
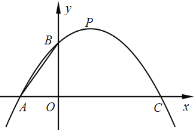
【题目】如图,二次函数![]() (a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(1)求 A、C 两点坐标;
(2)过点 B 作 BD∥x 轴交抛物线于 D,过点 P 作 PE∥AB 交 x 轴于 E,连接 DE,
①求 E 坐标;
②若 tan∠BPM=![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知∠C=90°,∠B=60°,点D在边BC上,过D作DE⊥AB于E.
(1)连接AD,取AD的中点F,连接CF,EF,判断△CEF的形状,并说明理由
(2)若BD=![]() CD.把△BED绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=
CD.把△BED绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=
查看答案和解析>>
科目:初中数学 来源: 题型:
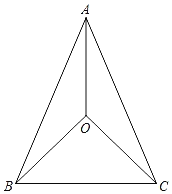
【题目】如图,在△ABC中,AB=AC,点O为∠BAC的平分线上一点,连接OB、OC.
(1)求证:OB=OC;
(2)若OA=OC,∠BAC=46°,求∠OCB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
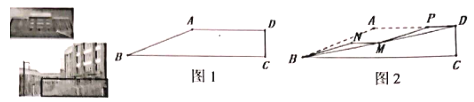
【题目】图1是我校闻澜阁前楼梯原设计稿的侧面图,![]() ,
,![]() ,楼梯
,楼梯![]() 的坡比为1:
的坡比为1:![]() ,为了增加楼梯的舒适度,将其改造成如图2,测量得
,为了增加楼梯的舒适度,将其改造成如图2,测量得![]() ,
,![]() 为
为![]() 的中点,过点
的中点,过点![]() 分别作
分别作![]() 交
交![]() 的角平分线于点
的角平分线于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,其中
,其中![]() 和
和![]() 为楼梯,
为楼梯,![]() 为平地,则平地
为平地,则平地![]() 的长度为_________
的长度为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
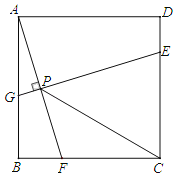
【题目】如图,已知四边形ABCD是边长为4的正方形,E为CD上一点,且DE=1,F为射线BC上一动点,过点E作EG⊥AF于点P,交直线AB于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45°时,BF=1;④PC的最小值为![]() ﹣2.其中正确的有( )
﹣2.其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com