
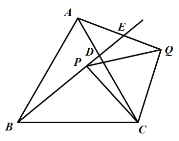
【题目】如图,在边长为 6 的等边△ABC 中,D 为 AC 上一点,AD=2,P 为 BD 上一点,连接 CP,以 CP 为 边,在 PC 的右侧作等边△CPQ,连接 AQ 交 BD 延长线于 E,当△CPQ 面积最小时,QE=____________.
【答案】![]()
【解析】
如图,过点D作DF⊥BC于F,由“SAS”可证△ACQ≌△BCP,可得AQ=BP,∠CAQ=∠CBP,由直角三角形的性质和勾股定理可求BD的长,由锐角三角函数可求BP的长,由相似三角形的性质可求AE的长,即可求解.
如图,过点D作DF⊥BC于F,
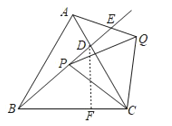
∵△ABC,△PQC是等边三角形,
∴BC=AC,PC=CQ,∠BCA=∠PCQ=60°,
∴∠BCP=∠ACQ,且AC=BC,CQ=PC,
∴△ACQ≌△BCP(SAS)
∴AQ=BP,∠CAQ=∠CBP,
∵AC=6,AD=2,
∴CD=4,
∵∠ACB=60°,DF⊥BC,
∴∠CDF=30°,
∴CF=![]() CD=2,DF=CF÷tan30°=
CD=2,DF=CF÷tan30°=![]() CF=2
CF=2![]() ,
,
∴BF=4,
∴BD=![]() =
=![]() =2
=2![]() ,
,
∵△CPQ是等边三角形,
∴S△CPQ=![]() CP2,
CP2,
∴当CP⊥BD时,△CPQ面积最小,
∴cos∠CBD=![]() ,
,
∴![]() ,
,
∴BP=![]() ,
,
∴AQ=BP=![]() ,
,
∵∠CAQ=∠CBP,∠ADE=∠BDC,
∴△ADE∽△BDC,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() ,
,
∴QE=AQAE=![]()
故答案为;![]() .
.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:
【题目】(3分)如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
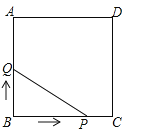
A.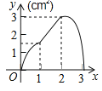 B.
B.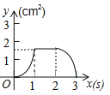 C.
C.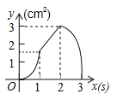 D.
D.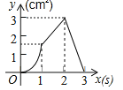
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了做好“营造清洁生活环境”活动的宣传,对本校学生进行了有关知识的测试,测试后随机抽取了部分学生的测试成绩,按“优秀、良好、及格、不及格”四个等级进行统计分析,并将分析结果绘制成如下两幅不完整的统计图:
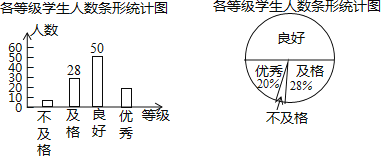
(1)求抽取的学生总人数;
(2)抽取的学生中,等级为“优秀”的人数为 人;扇形统计图中等级为“不合格”部分的圆心角的度数为 °;
(3)补全条形统计图;
(4)若该校有学生3500人,请根据以上统计结果估计成绩等级为“优秀”和“良好”的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
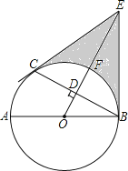
【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF = 2,BC = ![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
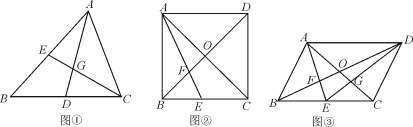
【题目】(1)证明推断:如图①,在△ABC中,D,E分别是边BC,AB的中点,AD,CE相交于点G,求证:![]() .
.
(2)类比探究:如图②,在正方形ABCD中,对角线AC、BD交于点O,E为边BC的中点,AE、BD交于点F,若AB=6,求OF的长;
(3)拓展运用:若正方形ABCD变为□ABCD,如图③,连结DE交AC于点G,若四边形OFEG的面积为![]() ,求□ABCD的面积.
,求□ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
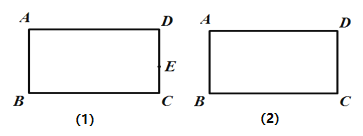
【题目】如图,四边形 ABCD 为矩形.
(1)如图1,E为CD上一定点,在AD上找一点F,使得矩形沿着EF折叠后,点D落在 BC边上(尺规作图,保留作图痕迹);
(2)如图2,在AD和CD边上分别找点M,N,使得矩形沿着MN折叠后BC的对应边B' C'恰好经过点D,且满足B' C' ⊥BD(尺规作图,保留作图痕迹);
(3)在(2)的条件下,若AB=2,BC=4,则CN= .
查看答案和解析>>
科目:初中数学 来源: 题型:
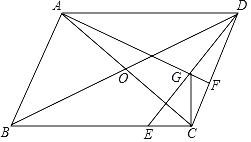
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是BC上一点,连接DE,点F在边CD上,且AF⊥CD交DE于点G,连接CG.已知∠DEC=45°,GC⊥BC.
(1)若∠DCG=30°,CD=4,求AC的长.
(2)求证:AD=CG+![]() DG.
DG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解
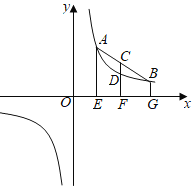
如图,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上,连接
的图象上,连接![]() ,取线段
,取线段![]() 的中点
的中点![]() .分别过点
.分别过点![]() ,
,![]() ,
,![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,![]() ,
,![]() ,
,![]() 交反比例函数
交反比例函数![]() 的图象于点
的图象于点![]() .点
.点![]() ,
,![]() ,
,![]() 的横坐标分别为
的横坐标分别为![]() ,
,![]() ,
,![]() .小红通过观察反比例函数
.小红通过观察反比例函数![]() 的图象,并运用几何知识得出结论:AE+BG=2CF,CF>DF,由此得出一个关于
的图象,并运用几何知识得出结论:AE+BG=2CF,CF>DF,由此得出一个关于![]() ,
,![]() ,
,![]() 之间数量关系的命题:若
之间数量关系的命题:若![]() ,则______.
,则______.
(2)证明命题
小东认为:可以通过“若![]() ,则
,则![]() ”的思路证明上述命题.
”的思路证明上述命题.
小晴认为:可以通过“若![]() ,
,![]() ,且
,且![]() ,则
,则![]() ”的思路证明上述命题.
”的思路证明上述命题.
请你选择一种方法证明(1)中的命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com