
【题目】如图,△ABC中,已知∠C=90°,∠B=60°,点D在边BC上,过D作DE⊥AB于E.
(1)连接AD,取AD的中点F,连接CF,EF,判断△CEF的形状,并说明理由
(2)若BD=![]() CD.把△BED绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=
CD.把△BED绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=
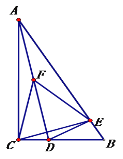
【答案】(1)等边三角形,见解析;(2)60°或135°
【解析】
(1)有直角三角形斜边的中线等于斜边的一半可得FC=FE,再证明∠CFE=60°即可;
(2)根据∠B=60°,∠DEB=90°,可知BD=![]() DE,又BD=
DE,又BD=![]() CD,则DC=DE,将△BED绕着点D逆时针旋转m°(0<n<180);分点B落在Rt△ABC的AB和AC上两种情况解答即可.
CD,则DC=DE,将△BED绕着点D逆时针旋转m°(0<n<180);分点B落在Rt△ABC的AB和AC上两种情况解答即可.
解:(1)△CEF为等边三角形,理由如下:
∵∠ACD=90°,∠B=60°,
∴∠CAB=30°
∵∠ACD=∠AED=90°,F是AD中点
∴CF=AF=DF=![]() AD, EF= AF=DF=
AD, EF= AF=DF=![]() AD
AD
∴CF=EF,∠CAF=∠FCA, ∠FAE=∠AEF,
∴∠CFD=∠CAF+∠FCA=2∠CAF, ∠EFD=∠EAF+∠AEF=2∠EAF,
∵∠CFE=∠CFD+∠EFD=2(∠CAF+∠EAF)=2∠CAB=60°
∴△CEF为等边三角形;
(2)①若点B落在AB边上的点M时,
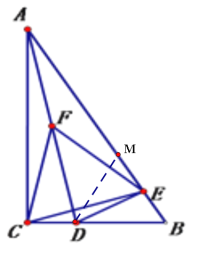
∵DB=DM, ∠B=60°
∴△DBM为等边三角形,m=∠BDM=60°
②若点B落在AC边上的点N时,
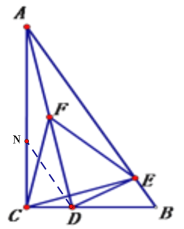
∵DB=DN=![]() CD, ∠C=90°
CD, ∠C=90°
∴△DBN为等腰直角三角形,
m=∠BDM=135°
综上所述,点B落在三角形的边上时,m=60°或135°.


科目:初中数学 来源: 题型:
【题目】如图, 已知点P为⊙O 外一点,PA、PB是⊙O的切线,切点分别是A、B,连接OP交AB于点C,交⊙O于点D,若PA=3cm, ∠APB=60°,则下列结论正确的有( )
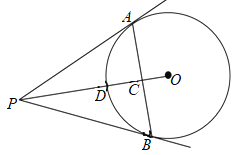
①AB⊥OP;②AC2=PC·OC;③若连接AD,BD,则∠ADB=120°;④PA,PB与劣弧AB围成的图形的面积是![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
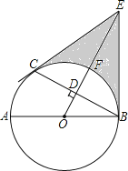
【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF = 2,BC = ![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
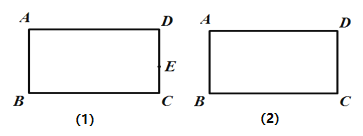
【题目】如图,四边形 ABCD 为矩形.
(1)如图1,E为CD上一定点,在AD上找一点F,使得矩形沿着EF折叠后,点D落在 BC边上(尺规作图,保留作图痕迹);
(2)如图2,在AD和CD边上分别找点M,N,使得矩形沿着MN折叠后BC的对应边B' C'恰好经过点D,且满足B' C' ⊥BD(尺规作图,保留作图痕迹);
(3)在(2)的条件下,若AB=2,BC=4,则CN= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快、慢两车分别从相距![]() 千米路程的甲、乙两地同时出发,匀速行驶.先相向而行,快车到达乙地后,停留
千米路程的甲、乙两地同时出发,匀速行驶.先相向而行,快车到达乙地后,停留![]() 小时,然后按原路原速返回,快车比慢车晚
小时,然后按原路原速返回,快车比慢车晚![]() 小时到达甲地,快、慢两车之间相距的距离
小时到达甲地,快、慢两车之间相距的距离![]() (千米)与出发后所用的时间
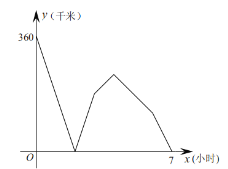
(千米)与出发后所用的时间![]() (小时)的关系如图所示,请问:在快车返回途中,快、慢两车相距路程为
(小时)的关系如图所示,请问:在快车返回途中,快、慢两车相距路程为![]() 千米时,慢车行驶了__________小时.
千米时,慢车行驶了__________小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
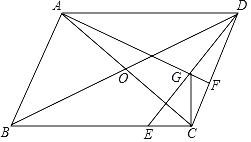
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是BC上一点,连接DE,点F在边CD上,且AF⊥CD交DE于点G,连接CG.已知∠DEC=45°,GC⊥BC.
(1)若∠DCG=30°,CD=4,求AC的长.
(2)求证:AD=CG+![]() DG.
DG.
查看答案和解析>>
科目:初中数学 来源: 题型:
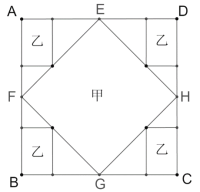
【题目】为了增加学校绿化,学校计划建造一块长为![]() 的正方形花坛
的正方形花坛![]() ,分别取四边中点
,分别取四边中点![]() ,构成四边形
,构成四边形![]() ,并计划用“两花一草”来装饰,四边形
,并计划用“两花一草”来装饰,四边形![]() 部分使用甲种花,在正方形
部分使用甲种花,在正方形![]() 四个角落构造4个全等的矩形区域种植乙种花,剩余部分种草坪,图纸设计如下.
四个角落构造4个全等的矩形区域种植乙种花,剩余部分种草坪,图纸设计如下.
(1)经了解,种植甲种花50元/![]() ,乙种花80元/
,乙种花80元/![]() ,草坪10元/
,草坪10元/![]() ,设一个矩形的面积为
,设一个矩形的面积为![]() ,装饰总费用为
,装饰总费用为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(2)当装饰费用为74880元时,则一个矩形区域的长和宽分别为多少?
(3)为了缩减开支,甲区域用单价为40元/![]() 的花,乙区域用单价为
的花,乙区域用单价为![]() 元/
元/![]() (
(![]() ,且
,且![]() 为10的倍数)的花,草坪单价不变,最后装饰费只用了55000元,求
为10的倍数)的花,草坪单价不变,最后装饰费只用了55000元,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
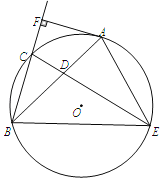
【题目】如图,已知AB是⊙O的弦,点C是弧AB的中点,D是弦AB上一动点,且不与A、B重合,CD的延长线交于⊙O点E,连接AE、BE,过点A作AF⊥BC,垂足为F,∠ABC=30°.
(1)求证:AF是⊙O的切线;
(2)若BC=6,CD=3,则DE的长为 ;
(3)当点D在弦AB上运动时,![]() 的值是否发生变化?如果变化,请写出其变化范围;如果不变,请求出其值.
的值是否发生变化?如果变化,请写出其变化范围;如果不变,请求出其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com