
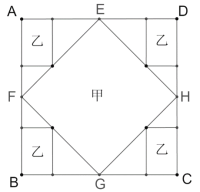
【题目】为了增加学校绿化,学校计划建造一块长为![]() 的正方形花坛
的正方形花坛![]() ,分别取四边中点
,分别取四边中点![]() ,构成四边形
,构成四边形![]() ,并计划用“两花一草”来装饰,四边形
,并计划用“两花一草”来装饰,四边形![]() 部分使用甲种花,在正方形
部分使用甲种花,在正方形![]() 四个角落构造4个全等的矩形区域种植乙种花,剩余部分种草坪,图纸设计如下.
四个角落构造4个全等的矩形区域种植乙种花,剩余部分种草坪,图纸设计如下.
(1)经了解,种植甲种花50元/![]() ,乙种花80元/
,乙种花80元/![]() ,草坪10元/
,草坪10元/![]() ,设一个矩形的面积为
,设一个矩形的面积为![]() ,装饰总费用为
,装饰总费用为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(2)当装饰费用为74880元时,则一个矩形区域的长和宽分别为多少?
(3)为了缩减开支,甲区域用单价为40元/![]() 的花,乙区域用单价为
的花,乙区域用单价为![]() 元/
元/![]() (
(![]() ,且
,且![]() 为10的倍数)的花,草坪单价不变,最后装饰费只用了55000元,求
为10的倍数)的花,草坪单价不变,最后装饰费只用了55000元,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)12,8;(3)50.
;(2)12,8;(3)50.
【解析】
(1)由题意,先得到四边形EFGH为正方形,然后求出面积,即可得到关系式;
(2)由(1)令y=74880,求出矩形的面积,然后利用方程,即可求出矩形的长和宽;
(3)根据题意,列出方程,然后得到![]() ,然后求出x的最大值,然后得到a的取值范围,即可得到答案.
,然后求出x的最大值,然后得到a的取值范围,即可得到答案.
解:(1)∵E,F,G,H分别为正方形ABCD各边的中点,
∴四边形EFGH为正方形,
且![]() ,
,
∴![]() ;
;
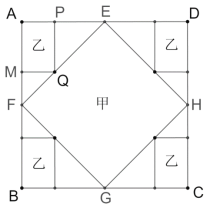
(2)令y=74880时,![]() ,
,
∴x=96
设PQ=PE=b,则AP=20-b,
∴![]() ,
,
解得:![]() ;
;
∴矩形的长为12,宽为8;
(3)由题意得![]()
∴![]()
∴![]() ,
,
∵![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
又∵a<80,且a为10的倍数,
∴a的最小值为50;


科目:初中数学 来源: 题型:
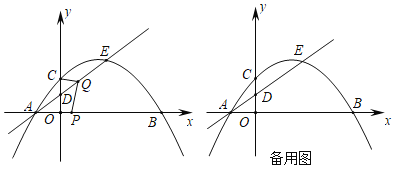
【题目】如图,在平面直角坐标系中,抛物线y=ax2+x+c与直线![]() 交于点A和点E,点A在x轴上.抛物线y=ax2+x+c与x轴另一个交点为点B,与y轴交于点C(0,
交于点A和点E,点A在x轴上.抛物线y=ax2+x+c与x轴另一个交点为点B,与y轴交于点C(0,![]() ),直线
),直线![]() 与y轴交于点D.
与y轴交于点D.
(1)求点D的坐标和抛物线y=ax2+x+c的函数表达式;
(2)动点P从点B出发,沿x轴以每秒2个单位长度的速度向点A运动,动点Q从点A出发沿射线AE以每秒1个单位长度的速度向点E运动,当点P到达点A时,点P、Q同时停止运动.设运动时间为t秒,连接AC、CQ、PQ.
①当△APQ是以AP为底边的等腰三角形时,求t的值;
②在点P、Q运动过程中,△ACQ的面积记为S1,△APQ的面积记为S2,S=S1+S2,当S=![]() 时,请直接写出t的值.
时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
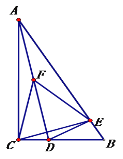
【题目】如图,△ABC中,已知∠C=90°,∠B=60°,点D在边BC上,过D作DE⊥AB于E.
(1)连接AD,取AD的中点F,连接CF,EF,判断△CEF的形状,并说明理由
(2)若BD=![]() CD.把△BED绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=
CD.把△BED绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:

(1)此次共调查了 名学生;
(2)扇形统计图中D所在扇形的圆心角为 ;
(3)将上面的条形统计图补充完整;
(4)若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
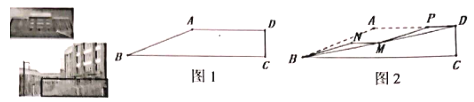
【题目】图1是我校闻澜阁前楼梯原设计稿的侧面图,![]() ,
,![]() ,楼梯
,楼梯![]() 的坡比为1:
的坡比为1:![]() ,为了增加楼梯的舒适度,将其改造成如图2,测量得
,为了增加楼梯的舒适度,将其改造成如图2,测量得![]() ,
,![]() 为
为![]() 的中点,过点
的中点,过点![]() 分别作
分别作![]() 交
交![]() 的角平分线于点
的角平分线于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,其中
,其中![]() 和
和![]() 为楼梯,
为楼梯,![]() 为平地,则平地
为平地,则平地![]() 的长度为_________
的长度为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,我国的空气质量得到了大幅度的提高.现随机调查了某城市1个月的空气质量情况,并将监测的结果绘制成如下的两幅不完整的统计图.
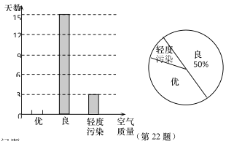
请根据图中提供的信息,解答下面的问题:
(1)本次调查中,一共调查的天数为_______天;扇形图中,表示“轻度污染”的扇形的圆心角为______度;
(2)将条形图补充完整;
(3)估计该城市一年(以365天计算)中,空气质量未达到优的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是规格为![]() 的正方形网格,请在所给网格中按下列要求操作:
的正方形网格,请在所给网格中按下列要求操作:
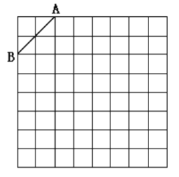
(1)请在网格中建立平面直角坐标系,使点![]() 坐标为
坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ;
;
(2)在第二象限内的格点上画一点![]() ,使点
,使点![]() 与线段
与线段![]() 组成一个以
组成一个以![]() 为底的等腰三角形,且腰长是无理数, 则
为底的等腰三角形,且腰长是无理数, 则![]() 点坐标是________,
点坐标是________,![]() 的周长是_________(结果保留根号);
的周长是_________(结果保留根号);
(3)画出![]() 以点
以点![]() 为旋转中心、旋转
为旋转中心、旋转![]() 后的
后的![]() ,连结
,连结![]() 和
和![]() ,试说出四边形
,试说出四边形![]() 是何特殊四边形, 并说明理由.
是何特殊四边形, 并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成如图表(成绩得分均为整数):
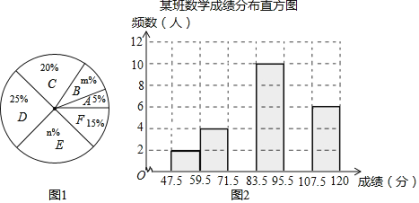
根据图表中提供的信息解答下列问题:
组别 | 成绩分组 | 频数 |
A | 47.5~59.5 | 2 |
B | 59.5~71.5 | 4 |
C | 71.5~83.5 | a |
D | 83.5~95.5 | 10 |
E | 95.5~107.5 | b |
F | 107.5~120 | 6 |
(1)频数分布表中的a= ,b= ;扇形统计图中的m= ,n= ;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 人,72分及以上为及格,预计及格的人数约为 人;
(3)补充完整频数分布直方图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com